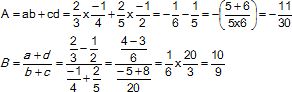
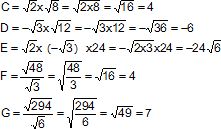
Mathématiques. Concours Aspts Metz 2014 . . . . Sachant que a = 2 /3, b = -1 / 4, c = 2 / 5 et d = -1 / 2, calculer ( donner le résultat sous forme d'une fraction irréductible). Calculer : Compléter les équations. 4x2 +9+12x =(2x+3)2. 81 +16x2 +72 x = (9+4x)2. 9x2-42x + 49= (3x-7)2. 49x2- 16=(7x+4)(7x-4) Un objet coûte 15 €. Il subit une hausse de 30 %. Quel est son nouveau prix ? 15 x1,3 = 19,5 €. Ce nouveau prix baisse de 30%. Retrouve t-on le prix initial ? 19,5 *0,7 = 13,65 €. Une fonction linéaire f est-elle que -3 a pour image 7. Quelle est le coefficient de cette fonction linéaire ? 7 / (-3) =-7 / 3. Quelle est l'image par la fonction f de -6 et +6 ? -6 x(-7 / 3 )= 14 ; +6 x(-7 / 3 )= -14. Quel est l'antécédent de 10 par la fonction f ? 10 x(-3) / 7 = -30 / 7. Soit un triangle ABC tel que AB = 3 rac. carrée (5), BC = 4 rac. carrée (5) et AC = 5 rac.carrée (5). Prouver que ce triangle est rectangle. AC2 = 25 x5 = 125 ; AB2 = 45 ; BC2 = 80; on constate que AC2 =AB2 +BC2 . 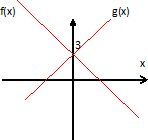Pour les fonctions affines définies par f(x) = -2x+3 et g(x) =2x+3), compléter le tableau puis faire une représentation graphique. x -4 0 4 f(x) 11 3 -5 g(x) -5 3 11 . . La route qui relie deux villes A et B comporte, de A vers B, une montée jusqu'au col de la Marmotte, puis une descente. Un cycliste part de A à 8h 00 pour se rendre à B. Sa vitesse moyenne est de 15 km/h en montée et de 45 km/h en descente. Il arrive à 9 h 30 min. Pour retourner de B à A, le cycliste roule à 15 km/h en montée et à 45 km/h en descente. Parti d à 9 h 45 min il arrive à 12 h15. Déterminer la distance de chaque ville au sommet du col. Soit x la montée et y la descente. Aller : x = 15 tM A  ; y = 45 tD A ; tM A+ tD A = 1,5 h. x / 15 + y / 45 = 1,5 soit 3x +y = 67,5. (1) Retour : y = 15 t'M R  ; x = 45 t'D R ; t'M R + t'D R =2,5 h. x / 45 + y / 15 = 2,5 soit x +3y =112,5. (2). Faire 3(1) -(2) : 8x =202,5-112,5 = 90 ; x = 11,25 km et y = 33,75 km. . . .

menu