Agitation thermique et diffusion. Second concours, école normale supérieure 2012 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.   . . . . Aux forces mécaniques agissant sur les protéines et les cellules s’ajoutent des forces thermiques issues de la collision avec l’eau et les autres molécules dans le fluide. Pendant chaque courte collision, le changement de quantité de mouvement des molécules de fluide induit une force spontanée sur l’objet frappé. Ces forces de collision sont appelées forces thermiques car leur amplitude est proportionnelle à la température du fluide. Le mouvement résultant est appelé mouvement thermique. Etant donné que ces forces sont dirigées de manière aléatoire, le mouvement est caractérisé par de fréquents changements de direction et est appelé diffusion. La diffusion d’une particule libre est également appelée mouvement Brownien. La diffusion est une forme de mouvement aléatoire qui est caractérisée par de fréquents et abrupts changements de direction. Le caractère aléatoire est le résultat de collisions avec les molécules du milieu, qui elles-mêmes se déplacent de manière aléatoire. La conséquence du mouvement aléatoire des molécules est qu’en moyenne les molécules ont tendance à se déplacer des régions de hautes concentrations vers les régions de basses concentrations. On peut ainsi montrer que, dans un système unidimensionnel, le flux de particule Jdiffusion(x), défini comme le nombre de molécules traversant une surface par unités de temps et de surface, est proportionnelle au gradient de concentration dc/dx et vérifie l’équation suivante : J diffusion(x) = -D dc/dx (x). avec c(x) la concentration de molécules à la position x (en molécules / m3) et D le coefficient de diffusion de la particule. 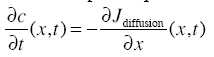Dans un système unidimensionnel, la redistribution d’une distribution non uniforme de particules au cours du temps est caractérisée par l’équation suivante : On définit la densité de probabilité p(x) de trouver une particule à la position x par : p(x) = c(x) / N avec N la concentration totale de molécules. On définit également le flux de densité de probabilité par : jdiffusion (x) = Jdiffusion (x)/N. On considère une particule se déplaçant dans un fluide avec un coefficient de frottement g et un coefficient de diffusion D. Une force externe F(x) agissant sur la particule diffusante cause sa dérive à la vitesse stationnaire vdérive(x). Un flux additionnel Jdérive(x) = vderive(x) . c(x) s’ajoute alors au flux Jdiffusion(x) résultant de la diffusion. 27. Donner, en justifiant par une analyse dimensionnelle, les unités du coefficient de diffusion D. [Jdiffusion(x))= molécules T-1 L-2 ; [dc/dx (x)] = molécules L-4 ; [D]=T -1 L2. 28. Écrire vdérive(x) en fonction de F(x) et des constantes du problème. A l'état stationnaire g vderive(x) =F(x). 29. En déduire l’expression du flux global de densité de probabilité j(x) = jdiffusion(x) + jdérive(x) (avec jdérive(x) = Jdérive(x) / N) en fonction de D, g, F(x) et p(x). j(x) =Jdiffusion / N + vderive(x) . c(x) / N. j(x) =Jdiffusion / N +F(x) c(x) / (Ng). j(x) =-D dc/dx (x)/ N + F(x) c(x) / (Ng). j(x) =-D dp/dx (x) + F(x) p(x) / g. 30. Montrer qu’à l’état stationnaire en présence d’une force F(x), la densité de probabilité p(x) vérifie l’équation suivante avec E une constante que l’on explicitera en fonction des constantes du problème et j0 le flux de densité de probabilité à l’état stationnaire. j0 /D= - dp/dx (x) + F(x) p(x) /(D g). On pose E =D g. dp/dx (x) - F(x) p(x) / E= -j0 /D. (1). 31. Montrer qu’à l’état stationnaire, la densité de probabilité peut s’écrire sous la forme : p(x) = [A − j0 / D B(x) ]exp( −U(x)/ E) où A est une constante, B(x) est une fonction de x vérifiant dB/dx = exp[U(x)/E], U(x) est l’énergie potentielle d’une particule à la position x associée à la force F(x) définie par F(x) = – dU(x) / dx. Solution générale de (1) sans second membre : p(x) =Cste exp(F(x)/E x). Solution particulière de (1) : p(x) = j0 E / (DF(x)). Solution générale de (1) : p(x) =A exp(F(x)/E x) + j0 E / (DF(x)) . p(x) =A exp(-U(x) / E ) + j0 E / (DF(x)) . B(x) = -E / F(x) exp[U(x) / E]. E / F(x) = -B(x) exp[-U(x) / E].   p(x) =A exp(-U(x) / E ) - j0 B(x)/ D exp(-U(x) / E). p(x) =(A- j0 B(x)/ D )exp(-U(x) / E). . . 32. A l’état stationnaire, la densité de probabilité suit la loi de Boltzmann qui stipule que : p(x) = 1 / Z exp(-U(x) / (kT)) où 1/Z est une constante permettant de satisfaire la condition d’unité, k est la constante de Boltzmann et T est la température. Déduire les conditions permettant de mettre en accord les deux expressions de p(x) données dans les questions 31 et 32. On identifie : 1 / Z = A- j0 B(x)/ D et E = kT. 33. En déduire (i) la valeur du flux de densité de probabilité à l’état stationnaire j0 et (ii) l’expression du coefficient de diffusion D en fonction de k, T et g. E =D g =  kT ; D = kT / g. j0 = (A-1/ Z ) D / B(x). 34. En s’aidant de la formule de la constante de frottement g = 6 p r h, expliquer comment varie le coefficient de diffusion d’une particule en fonction de sa taille et en fonction de la viscosité h du milieu. D = kT / ( 6 p r h). Le coefficient de diffusion diminue si la taille de la particule et la viscosité du milieu augmentent. 35. Un ion Na+ a un coefficient de diffusion DNa de 1,33 × 10–9 SI à 25°C. Quel est le rayon apparent de l’ion Na+ ? On prendra h = 0,89 mPa.s et kT = 4,12 × 10–21 J. r = kT / ( 6 pDNa h) = 4,12 10-21 / (6*3,14 *1,33 10-9 *0,89 10-3)=1,8 10-10 m. 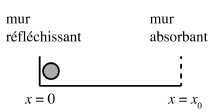On considère une boite unidimensionnelle dans laquelle est positionné un mur réfléchissant à x = 0 et un mur absorbant à x = x0. Par définition, p(x0) = 0. On place une molécule à x = 0. On définit le temps de premier passage t0 comme le temps moyen nécessaire à une particule relâchée en x = 0 pour parcourir la distance x0. Une façon de calculer le temps de premier passage est d’imaginer qu’il y a beaucoup de molécules dans la boite, et que chaque fois qu’une molécule touche le mur absorbant elle est instantanément replacée à l’origine. Au bout d’un moment, la distribution des molécules atteint un état stationnaire et on peut montrer que dans ce cas le temps de premier passage t0 peut s’écrire : t0 = 1 /j(x0 ) 36. Montrer qu’à l’état stationnaire en l’absence de force externe : p(x) = − 2x / x02 + 2 / x0. p(x) =(A- j0 B(x)/ D )exp(-U(x) / E). En absence de force externe : U(x) =0 ; exp(-U(x) / E) = 1 et B(x) = x +Cste. p(x) =A- j0 (x+Cste)/ D. p(x0) =0 = A- j0 x0/ D -j0 / D Cste ; A-j0 / Dcste  = j0 x0 / D. p(x) = j0 x0 / D - j0 x / D. On pose x20 = 2D /j0. p(x) = − 2x / x02 + 2 / x0. 37. En déduire l’expression de t0 en fonction de x0 et D. j(x) =-D dp/dx (x) = 2D/ x02  ; t0 = 1 /j(x0 ) =x02  / (2D). 38. 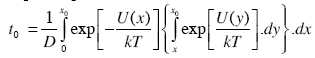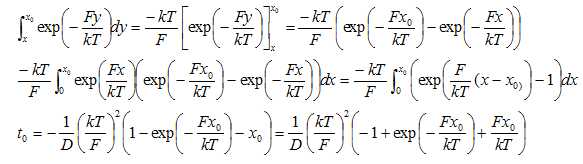Une solution générale pour le temps de premier passage t0 en présence d’une force externe F(x) est donnée par l’équation suivante : Montrer que l’expression du temps de premier passage t0 lorsque l’on applique une force F(x) = F constante s’écrit : 39. On considère une protéine de coefficient de diffusion 67 × 10–12 SI. Combien de temps mettra-t-elle pour parcourir 40 nm en l’absence de force externe ? t0 =x02  / (2D) =(40 10-9)2 /(2*67 × 10–12) =1,2 10-5 s. 40. On suppose maintenant une force F = 1 pN. Combien de temps mettra la protéine pour parcourir 40 nm si elle se déplace dans le sens de la force ? Combien de temps mettra la protéine pour parcourir 40 nm si elle se déplace dans le sens inverse de la force. Commenter. On prendra kT = 4,12 × 10–21 J. (kT/F)2 / D =(4,12 10-21 /  10-12)2/(67 × 10–12)=2,53 10-7. exp(-Fx0/(kT)) = exp(-10-12 *40 10-9/(4,12 × 10–21))~ 6,075 10-5 ; Fx0/(kT) =10-12 *40 10-9/(4,12 × 10–21 )=9,709 ;  t0 ~ 2,53 10-7*8,709=2,2 10-6 s. Déplacement en sens inverse de la force : remplacer F par -F. exp(+Fx0/(kT)) = exp(+10-12 *40 10-9/(4,12 × 10–21))~ 1,65 104 ; -Fx0/(kT) =10-12 *40 10-9/(4,12 × 10–21 )= -9,709 ;  t0 ~ 2,53 10-7*1,645 104=4,2 10-3 s. .

menu