Conductimétrie :
dosage acide base, solubilité.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Dosage
conductimétrique d'un acide fort par une base forte.
On se propose de doser Va = 100 mL d'une solution d'acide
chlorhydrique de concentration ca = 0,02 mol/L ( 20 mol m-3) par une
solution de soude de concentration cb = 0,5 mol/L( 500 mol m-3). On fait l'hypothèse que le volume V de la solution varie très peu. V ~Va.
lH+= 35 10-3S m2 mol-1 ; lHO-= 20 10-3S m2 mol-1 ; lNa+= 5 10-3S m2 mol-1 ; lCl-= 7,6 10-3S m2 mol-1 ;
1. Donner l'expression de
la conductivité en fonction du volume Vb de base versé avant
l'équivalence. Justifier qualitativement et quantitativement son évolution.
L'ion hydroxyde est en défaut. Ions présents : H+; Cl-, Na+.
[H+] = (Vaca-Vbcb)
/ V ; [Cl-]=Vaca
/ V ; [Na+]=Vbcb
/ V.
Conductivité : s
=( lH+(Vaca-Vbcb) + lCl-Vaca +lNa+Vbcb ) / V.
s =(( lH++lCl-)Vaca+(lNa+-lH+)Vbcb ) / V.
s =(35+7,6)10-3*20 +(5-35) 10-3*500 /0,1 Vb.
s =0,852-150 Vb en S m-1 et Vb en litre.
On observe une décroissance de la conductivité.
Du point de vue de la conductivité, tout revient à remplacer l'ion H+ par l'ion Na+.
Or lNa+<<lH+.
2. Donner l'expression de la conductivité
en fonction du volume Vb de base versé après l'équivalence. Justifier qualitativement et quantitativement son évolution.
L'ion H+ est en défaut. Ions présents : HO-; Cl-, Na+.
[HO-] = (Vbcb-Vaca)
/ V ; [Cl-]=Vaca
/ V ; [Na+]=Vbcb
/ V.
Conductivité : s
=( lHO-(Vbcb-Vaca) + lCl-Vaca +lNa+Vbcb ) / V.
s =(( lHO-+lNa+)Vbcb+(lCl- -lHO-)Vaca ) / V.
s =(20+5)10-3*500Vb /0,1+(7,6-20)10-3*20.
s =125Vb - 0,248.
On observe la croissance de la conductivité.
On ajoute des ions hydroxyde et des ions sodium : la conducctivité croît.
3. Donner l'expression de la conductivité à l'équivalence.
Ions présents à l'équivalence :
Cl-, Na+.
Conductivité : s =( lCl-Vaca +lNa+Vb
Ecb ) / V.
De plus : Vaca
= Vb Ecb.
s =( lCl- +lNa+)Vb
Ecb / V.
s =(7,6+5)10-3 *500 /0,1 VbE = 63 VbE.
|
| .
. |
|
|
4. Construire les graphes s = f(Vb) et déterminer le volume équivalent ainsi que la conductivité à l'équivalence.
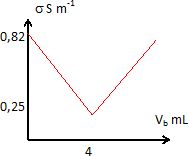
L'équivalence est déterminée par l'intersection des deux segments de droite.
s =0,852-150 VbE =125VbE - 0,248.
VbE =(0,852+0,248 )/ 275 = 0,0040 L = 4,0 mL.
Conductivité à l'équivalence : 63*0,0040 = 0,25 S m-1.
5. L'hypothèse de départ est-elle justifiée ?
Le volume de soude ajouté à l'équivalence est très inférieur au volume de solution acide initiale.
Va ~Va + VbE. L'hypothèse est donc valide.
|
|
|
|
Mesure de la
solubilité par conductimétrie.
La mesure, par conductimétrie, de la résistance électrique d'une
solution de iodate de calcium saturée (Ca (IO3)2), à température ambiante, donne R
= 2420 ohms. Dans les mêmes conditions, la mesure de la résistance
d'une solution étalon de KCl, de conductivité égale à sref = 1,0
S m-1, donne Rref = 85 ohms.
lCa2+
= 11,89 mS m2 mol-1 ; lIO3-
= 4,05 mS m2 mol-1.
CaIO3(s) = Ca2+ aq + 2IO3-aq. (1)
1. Exprimmer de deux ùmanières différentes
la conductivité de la solution saturée en iodate de calcium à 25°C en fonction des données puis la calculer.
La solution est électriquement neutre : 2[Ca2+
]=[IO3- ]
On pose s = [Ca2+
] ; [IO3- ] = 2s.
s
=lCa2+
[Ca2+ ]+lIO3-[IO3- ]
=( lCa2++2lIO3- ) s ;
Conductivité et conductance sont proportionnelles ; la conductance est l'inverse d'une résistance.
par suite : R = k /s
avec k une constante.
Rref
= k / sref
; k = Rref sref ; s =Rref
sref
/ R.
s
= 85 / 2420 * 1,0 =3,5 10-2 S m-1.
2. Exprimer la solubilité en fonction des données puis la calculer.
( lCa2++2lIO3- ) s = Rref
sref
/ R ; s = Rref
sref
/(R( lCa2++2lIO3- )).
s =85*1,0/(2420 (11,89 +4,05)10-3)
= 2,2 mol m-3 = 2,2
10-3 mol/L.
3. Donner l'expression de la constante Ks
de la réaction (1) puis donner la valeur de pKs à 25°C.
Ks =[Ca2+
] [IO3-]2
=4 s3 = 4( 2,2 10-3)3
=4,28 10-8 ; pKs = 7,37.
|
|
|
|