QCM
Thermodynamique. Concours CPR 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Mélange de gaz
parfaits.
On considère deux gaz parfaits G1 et G2 de même
atomicité, de masses molaires M1 et M2 et de
chaleur massiques à volume constant Cv1 et Cv2.
On enferme n1 = 2 mol de G1 et n2 = 1
mol de G2 respectivement dans deux récipients de volumes V1
= 2 L et V2 = 1 L portés aux températures T1 =
1000 K et T2 = 700 K. Les pressions des gaz sont p1
et p2.
Les récipients indilatables, imperméables à la chaleur et de capacités
calorifiques négligeables sont réunis par un tube de volume négligeable
portant un robinet. Le système n'échange ni travail, ni chaleur avec
l'extérieur. On ouvre le robinet et on laisse l'équilibre s'établir.
12. La température
commune des deux gaz est :
On note T la température finale et pour un
gaz monoatomique Cv = 1,5R /M.
Variation d'énergie interne de G1 : n1M1
Cv1( T-T1) = 1,5 R n1( T-T1).
Variation
d'énergie interne de G2 : n2M2 Cv2(
T-T2) = 1,5 R
n2( T-T2).
La variation d'énergie interne de l'ensemble est nulle.
n1( T-T1) +n2(
T-T2) = 0.
T = (n1T1 +n2T2) / (n1+n2)=(2000
+700) / 3 = 900 K. Réponse B.
13.
La pression commune au mélange des deux gaz est :
P(V1+V2) =(n1+n2)RT ; P =
3*8,3*900 / (3 10-3)~7,5 106 Pa. Réponse D.
Rendement d'un cycle moteur.
Un
gaz parfait décrit un cycle moteur ABCD constitué de deux
transformations adiabatiques réversibles AB et CD séparées par deux
transformations isobares DA et BC aux pressions pA et pB avec pB > pA. g = 1,4 et pB / pA = 8.
14. Le rendement du cycle vaut :
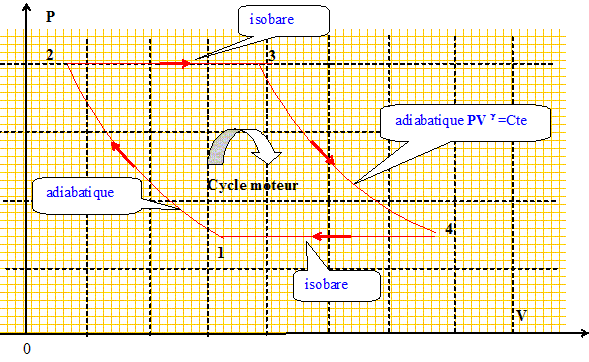
Rendement = travail récupéré
divisé par l'énergie
prélevée à la source
chaude.
La variation d'énergie interne du gaz est
nulle sur le cycle : DUcycle
= 0 = W + Q.
W = -Q avec
Q23>0 (
reçu par la source chaude) et
Q41<0 ( cédé à
la source froide)
W = Q41-
Q23 ;
h
=
(Q23+Q41
) / Q23 ; h
= 1+Q41 /
Q23.
(1) à (2), transformation
adiabtique réversible :
P11-g
T1g
=P21-g
T2g
;
T2
=
T1[P1
/P2
](1-g)
/ g
.
(3) à (4), transformation
adiabtique réversible :
P31-g
T3g
=P41-g
T4g
;
Or P3 = P2 et P4 =
P1 : les transformations 2-->3 et 4-->1
sont isobares ; par suite :
T4
=
T3[P2
/P1
](1-g)
/ g
.
Q41 / Q23
= (T1-T4) /
(T3-T2) ; remplacer
T2 et T3 par leur expression
:
T3-T2
=T4
[P1
/P2](1-g)
/
g-T1[P1
/P2
](1-g)
/ g =
(T4
-T1)[P1
/P2
](1-g)
/ g .
Q41 / Q23
=
-1/[P1
/P2
](1-g)
/ g =
-[P2
/P1
](1-g)
/ g ;
h
=1-[P2
/P1
](1-g)
/ g
.
h = 1-8-0,4 / 1,4 =0,448. Réponse C.
|
| .
. |
|
|
Variation d'entropie de l'eau.
Une masse de 1 kg de vapeur d'eau se trouve initialement à la température t1 = 50°C sous la pression de vapeur saturante à 50°C, p1 =1,23 104 N m-2. Cette masse est amenée à la température t2 = 150°C sous la pression de vapeur saturante à 150°C, p2 = 4,78 105 N m-2. La chaleur massique de la vapeur sous pression constante est C = 1,97 kJ kg-1°C-1.
15. La variation d'entropie de cette masse de vapeur entre les deux états est :
DS = nCp ln (Tf / Ti) -nR ln(Pf / Pi) avec n = 1000 /18 = 55,55 mol.
DS =1,97 103 ln(150+273) / (50+273) -55,55*8,3 ln(47,8 / 1,23)]~ -1,16 kJ K-1.
Réponse D.
|
|
|
|
Pentes adiabatique et isotherme.
Une masse m de gaz parfait se trouve dans les conditions (p0, V0, T0) , état A. On fait subir à ce gaz séparément les transformations suivantes :
- une compression isotherme jusqu'à la pression p1 ( état B) ;
- une compression adiabatique jusqu'à la pression p1( état C).
Donnée : g = 1,4.
16. En A les pentes [dP/dV]adia et [dP/dV]isoth sont telles que :
P= nRT / V ; ln P + ln V = ln (nRT) = constante.
dP/P + dV/V = 0 ; [dP/dV]isoth = -P / V.
Adiabatique réversible : PVg = constante.
dP/P + g dV/V = 0 ; [dP/dV]adia = -g P/V = -g [dP/dV]isoth.
Réponse C.
|
|
|
|
