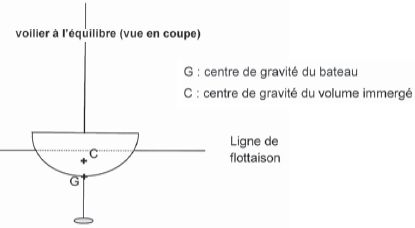
Stabilité et propulsion du voilier. Concours Caplp maths sciences 2015. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Stabilité du voilier. Le voilier est écartéde sa position d'équilibre. On cherche à déterminer si le bateau revient à sa position d'équilibre stable lorsque la contrainte mécanique responsable de son nclinaison est relâchée. L'action du vent ne sera pas prise en compte. Effectuer un  bilan des forces lorsque le bateau est dans sa position d'équilibre stable. Le bateau est soumis à son poids, appliqué en G, verticale vers le bas, valeur P= mg et à la poussée d'Archimède, appliquée en C, verticale vers le haut, valeur égale au poids. On suppose que le bateau est dans une configuration hors équilibre ( après avoir écarté le bateau de sa position d'équilibre, la contrainte est relâchée ). L'angle de gite est égal à q. Le bilan des forces est identique à celui de la question précédente. Tracer sur le schéma les vecteurs forces correspondants. 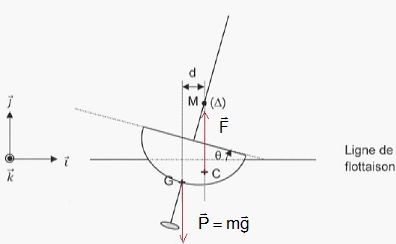Donner les expressions des moments des forces par rapport à l'axe D passant par le métacentre M en fonction  des paramètres suivants ( m : masse du bateau, g : champ de pesanteur, d : longueur indiquée ). Le sens positif est par convention le sens trigonométrique. L'effet  de rotation de la pousée est nulle, la direction de cette force rencontre l'axe de rotation D. Le poids a pour effet la rotation dans le sens positif. Mpoids = mg d. La somme vectorielle des forces précédentes est nulle. Comment expliqueriez-vous à des élèves qu'il sagit tout de même d'une situation hors équilibre ? Un solide est dans une situation d'équilibre lorsque deux conditions sont réunies :  La somme vectorielle des forces appliquées à ce solide est nulle et lorsque les effets de rotation des forces se compensent ( la somme algébrique des moments des forces par rapport à l'axe de rotation est nulle). La  courbe de stabilité suivante représente le moment du poids par rapport à l'axe D en fonction de l'angle de gîte q. Un angle de gîte nul correspond à une situation stable. Déterminer graphiquement la valeur de l'angle de gîte qAVS correspondant à l'angle limite au delà duquel le bateau chavire et préciser quel est l'intervalle des angles de gîte pour lesquels le voilier peut revenir à sa position d'équilibre. 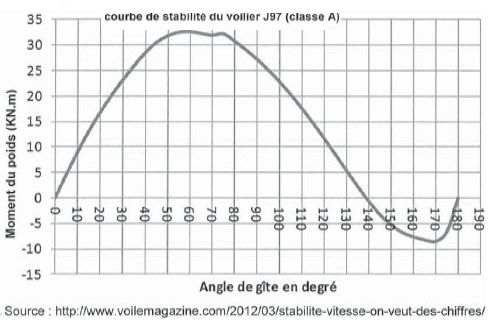Lorsque le moment du poids par rapport à l'axe D devient négatif, le bateau chavire.  qAVS = 140°. Pour un angle de gîte compris entre 0 et 140° ( valeur exclue) , le moment du poids est positif : le voilier peut revenir à sa position d'équilibre. . . Le moment du poids est également appelé moment redressant. Pour quel intervalle d'angle de gîte cette expression n'est pas appropriée ? Lorsque le moment du poids est négatif le bateau chavire. L'angle de gîte est compris entre 140 ° et 180°. q= 180° est une position d'équilibre, mais le bateau est retourné. L'angle de gîte qAVS correspond-il à une position d'équilibre ? Justifier. Cet éventuel équilibre est-il stable ? ( aucun développement mathématique n'est demandé). Pour cet angle de gîte, le centre de gravité et le centre de pousée sont sur la même verticale, celle passant par le métacentre M. Les moments des forces sont nuls. Il s'agit d'une position d'équilibre instable. A partir de cette position, si on écarte un peu plus le voilier, celui-ci chavire. Détermination expérimentale de la poussée d'Archimède. Décrire une expérience permettant de déterminer une mesure de cette poussée. Suspendre une masse m = 300 g à un dynamomètre. La poussée due à l'air étant négligeable, la valeur lue donne le poids P. Immerger complètement le solide de masse m dans un liquide. Le dynamomètre indique le poids apparent. La différence des deux lectures donne la valeur de la poussée. Autre expérience. Placer un vase à trop-pein ( rempli d'eau jusqu'au tube d'écoulement )et un solide sur une balance. Immergé le solide dans le vase : récupérer l'eau qui s'écoule par le trop-plein dans un flacon gradué. Mesurer ce volume d'eau écoulé. Peser le volume d'eau écoulé sur une balance tarée. Le poids du volume d'eau déplacé est égal à la poussée d'Archimède. Propulsion et chavirage du voilier. On suppose que le mouvement du voilier est rectiligne uniforme. Les mouvements de rotation du bateau sont supposés nuls. La direction du voilier est différente de celle de son axe longitudinal de symétrie. L'angle  entre ces deux directions correpond à l'angle de dérive noté ad. L'angle de gîte du bateau est supposé constant. L'action du vent est désormais prise en compte. Faire l'inventaire des forces mécaniques exercée sur le voilier et donner la relation entre les forces correspondantes. Justifier. 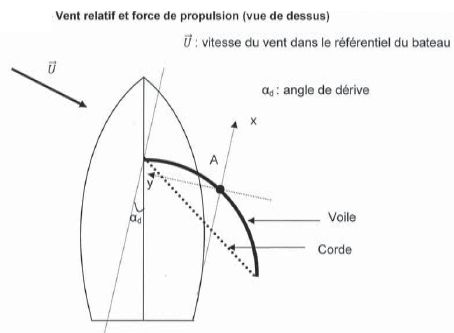. Au poids et à la poussée, il faut ajouter une force due au vent. Le mouvement du bateau étant rectiligne uniforme, la première loi de Newton indique que la somme vectorielle de ces forces est nulle. Expliquer pour quelle raison le référentiel du bateau est galiléen. Un référentiel terrestre peut être considéré comme galiléen ; il en est de même pour tout référentiel animé d'un mouvement rectiligne uniforme par rapport au référentiel terrestre. La vitese du vent est modifiée au voisinage de la voile. Il existe une couche limite à proximité de la voile, dans laquelle les phénomènes de viscosité ne sont pas négligeables. Cette couche limite permet une circulation de fluide induite par la forme asymétrique de la voile. La vitesse de l'air au voisinage de la voile est donc modèlisée par la composition d'un écoulement d'air rectiligne et d'un écoulement tournant autour de la voile. 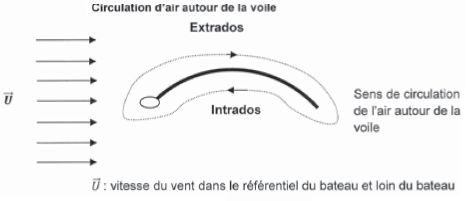Comparer la vitesse des particules fluides aux voisinages de l'intrados et de l'extrados. L'extrados étant bombé, la distance à parcourir par les molécules d'air est supérieure à celle que doivent parcourir les molécules d'air suivant l'intrados. Le filet d'air longeant l'extrados va circuler plus vite que celui longeant l'intrados. Justifier à l'aide de la relation de Bernoulli la présence d'une force aérodynamique. Rappeler la signification physique de la relation et ses conditions d'application. Relation de Bernoulli : p + rgz + ½rv² = constante. g représente la valeur du champ de pesanteur terrestre. Cette relation peut être applicable à tout le fluide si : le fluide est incompressible (r constant), "parfait" ( viscosité nulle), en régime permanent et sans transfert de chaleur. Interprétation énergétique de cette relation : Cette relation traduit la conservation de l'énergie le long d'une ligne de courant. La loi de Bernoulli indique qu'à altitude égale la pression du fluide diminue si sa vitesse augmente. Le résultat est une force aérodynamique faisant avancer le bateau. Expliquer en langage simple ce que les élèves doivent retenir de l'effet Venturi. Le débit est constant : si le diamètre de la canalisation diminue, la vitesse croît. L'énergie se conserve le long d'une ligne de fluide : il y a dépression dans un fluide dans une zone où les particules sont accélérées. 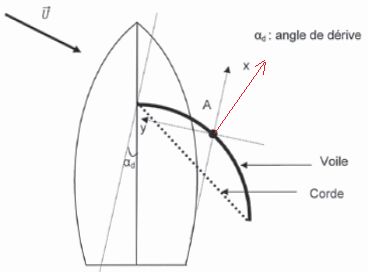En supposant que la direction de la force aérodynamique est perpendiculaire à la corde de la voile, tracer au point A, sans souci d'échelle, mais en le précisant et en le justifiant le sens de cette force. La force aérodynamique s'exerce des hautes vers les basses pressions. La composante parallèle au mouvement du bateau de cette force correspond à la force de propulsion du bateau alors que la composante perpendiculaire est la force de dérive notée FD. Une force anti-dérive, notée FA et opposée à FD s'exerce sur les appendices du voilier, fixées sous la coques ( quille, safrans, dérives ). Ces deux forces forment un couple appelé couple de chavirage. Justifier ce nom. 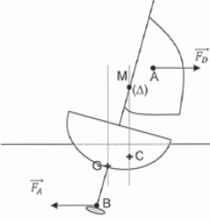L'effet de ce couple de forces est la rotation dans le sens anti-trigonométrique. Il tend à faire chavirer le voilier. Pour un mouvement du bateau rectiligne uniforme, déterminer, à partir de la courbe de stabilité ci-dessus, un ordre de grandeur de l'angle de gîte correspondant au moment de ciuple de chavirage maximum. Le voilier est soumis au couple de redressement ( dû au poids) et au couple de chavirage. Pour un mouvement rectiligne uniforme, la somme algébrique des moments de ces deux couples est nul ( les effets des couples se neutralisent ). Le couple de chavirage est maximum lorsque le moment du poids est maximal ( q voisin de 60°). 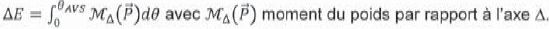L'expression de l'énergie nécessaire pour faire chavirer le navire est la suivante : Expliquer de quelle manière il est possible d'évaluer l'énergie nécesssaire pour faire chavirer le bateau, à partir de la courbe de stabilité. L'énergie nécessaire au chavirement est égale à l'aire positive de la surface comprise entre la courbe de stabilité et l'axe horizontal, pour un angle de gîte compris entre 0 et qAVS.. Le réglement IMOCA impose que l'aire positive sous la courbe de stabilité doit être au minimum 5 fois supérieure à l'aire négative. Interpréter cet aspect du réglement en termes énergétiques. La surface sous la courbe est l’intégrale du moment redressant, c’est le travail nécessaire pour incliner le navire jusqu’au point de chavirement. Ce travail doit être grand pour le bateau droit, il est doit être le plus petit possible pour le bateau chaviré. Le moment du poids est appelé moment redressant. Le couple de redressement maximum autorisé est égal à 320 kN m. Expliquer pourquoi cette grandeur est limitative de la puissance motrice du voilier en mouvement rectiligne uniforme. Dans un mouvement rectiligne uniforme le moment du couple de chavirage est égal au moment du couple de redressement. La force de propulsion est égale à FD / tan ad.

menu