Mesure
de la distance angulaire entre les deux composantes d'une étoile
double.
Agrégation 2004
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Interférences
lumineuses à deux ondes.
On utilise le modèle scalaire de la lumière. Soient s1(M,t)
et s2(M,t) les amplitudes de deux ondes
monochromatiques synchrones reçues en un point M quelconque du champ
d'’interférences :
s1(M,t) = s10 cos (wt+f1)
; s2(M,t) = s20 cos (wt+f2)
Les phases f1
et f2
dépendent de la position du point M.
On admet que l'’intensité lumineuse I(M) mesurée par un détecteur placé
en M est proportionnelle à la valeur moyenne temporelle du carré de
l’'amplitude de l’'onde reçue en ce point. On a donc :
I1(M) = k <s1(M,t)2>
et I2(M) = k <s2(M,t)2>
I(M) = k <s(M,t)2> avec s(M,t) = s1(M,t)+s2(M,t).
Exprimer
I1(M) en
fonction de (s10)2.
I1(M)
= k <s1(M,t)2>
=k<s210
cos2 (wt+f1)>=
½k s210.
Donner
l’'expression de s(M,t)2, puis
celle de I en fonction de I1(M) et I2(M),
intensités de chacune des ondes, et du déphasage f = f2 - f1.
s2(M,t)
= s210
cos2 (wt+f1)
+s220
cos2 (wt+f2) +2s10 s20
cos (wt+f1)cos (wt+f2).
s2(M,t)
= s210
cos2 (wt+f1)
+s220
cos2 (wt+f2) +s10 s20 cos (2wt+f1+f2)cos (f1-f2).
I(M)=k<s2(M,t)>= ½ ks210
+ ½ ks220
+½ks10 s20 <cos (f)>.
I(M)=I1(M)
+I2(M)
+2(I1(M)I2(M))½<cos (f)>.
À quelle
condition observe-t-on des interférences lumineuses en M
?
Les interférences sont observés si f est constant au
cours du temps. On dit alors que les
ondes sont cohérentes.
Que vaut
I(M) pour des ondes incohérentes ? Commenter.
<cos (f)> =0 et I(M)=I1(M)
+I2(M).
Les intensités des sources s'ajoutent en tout point M du champ.
On note I0
la valeur commune à I1(M) et I2(M).
Que
vaut I(M) pour des ondes cohérentes ?
I(M)=2I0(M)+2I0(M)<cos (f)> = 2I0(M)(1+<cos (f)>).
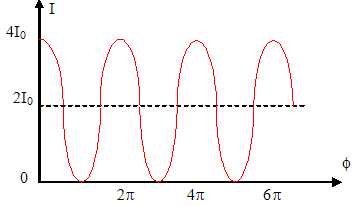
Tracer
I(M) en fonction du déphasage f dans le
cas où I1(M) = I2(M). Pour
quelles valeurs de f
l’'intensité est-elle maximale ?
L'intensité est maximale pour f
= 2 p
p avec p entier.
|
| .
. |
|
|
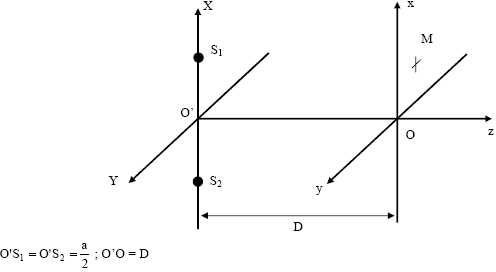
Mesure
de la distance angulaire entre les deux composantes d’une étoile double.
On réalise l’'expérience des trous de Young, distants de a, en lumière
monochromatique. On observe les interférences sur un écran placé dans
le plan focal image d’une lentille convergente (L) de distance focale f
’. La source lumineuse qui éclaire les trous de Young est une étoile E1
située à l’infini dans la direction de l’'axe optique de (L),
d’'intensité
lumineuse I0. La longueur d’onde de la lumière
émise est l.
Faire
un schéma représentant les rayons lumineux qui interfèrent en un point
M d'’abscisse x de l’'écran.
On utilise la lentille dans les conditions de Gauss. Pourquoi
?
Dans ces conditions, la lentille est stigmatique pour tous les couples
de points conjugués.
Calculer
la différence de marche en M en fonction de a, x et f ’ , puis
l’'intensité lumineuse I1(x) en
fonction de I0, l, a, x et
f ’.
Pour les petits angles ( conditions de Gauss ), tan q ~sin q ~q radian.
d
= aq ; q
~x / f ' ; d = a x / f ' ;
interfrange i = l f
' /a.
I1(x)=
2I0(M)(1+cos (f))=2I0(M)(1+cos (2pd/l))= 2I0(M)(1+cos (2px / i)).
|
.
|
|
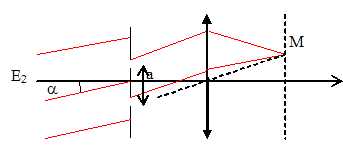
Une étoile E2
est à l'’infini dans la direction a
par rapport à l’'axe optique de (L). L'’angle a est très petit.
Faire
un schéma en représentant les rayons lumineux qui interfèrent en un
point M d'’abscisse x de l’'écran.
Calculer
la différence de marche en M en fonction de a, x, f ’ et a, puis
l’'intensité lumineuse I2(x) en
fonction de I0, l, a, x, f
’ et a.
Commenter le résultat.
Avant les fentes d'Young, la différence de marche est d' = ± a a.
d +d' = a x / f ' ± a a.
I2(x)=2I0(M)(1+cos (2p / l (a x / f ' ± a a)))= 2I0(M)[1+cos (2p a/( l f ' )( x ± a f '))].
La figure d'interférences est identique à la précédente, mais décalée
de x0 = ±a f '.
On étudie l’'étoile double δOrionis dont les deux composantes E1
et E2 ont même éclat. E1
et E2 éclairent maintenant le dispositif.
On augmente progressivement la distance séparant les trous d'Young.
Montrer
simplement que l'’intensité devient uniforme pour une valeur
particulière a1 de a.
On prend l
= 550 nm et a1 = 28,4 cm ; calculer a en radians.
I = I1+I2.
On observe le premier brouillage des franges ( intensité uniforme )
pour x0
= ½ i ; a
f ' = ½ i = l f ' /(2a1).
a = l /(2a1)
= 550 10-9 / (2*0,284)=9,68 10-7
rad.
|
|
|