Mouvement d'une planète autour d'une étoile, référentiel barycentrique. Agrégation 2004 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . On considère une étoile de centre E, de rayon R, de masse M dont la répartition est à symétrie sphérique et une planète de centre P assimilée à un point matériel de masse m très petite devant M. Le système étoile-–planète est supposé isolé. Le référentiel (RE), centré en E est considéré comme galiléen dans cette question. Déterminer le champ de gravitation créé par l'’étoile en un point situé à une distance r > R. Justifier qu’il est identique à celui créé par une masse ponctuelle en E. L'étoile est à répartition sphérique de masse. Le champ de gravitation est invariant par rotation : ce champ est donc radial. Ecrire le théorème de Gauss pour la gravitation, la surface fermée sera une sphère de centre E et de rayon r. Le vecteur unitaire est orienté de E vers P. 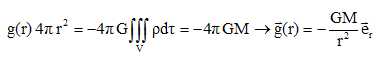Tout se passe comme si la masse de l'étoile était concentrée en son centre. Exprimer la force exercée par l’étoile sur la planète. 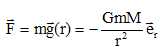Justifier soigneusement que le mouvement de P est plan. Ecrire le théorème du moment cinétique en E, dans le repère RE, dans le cas d'une force centrale. 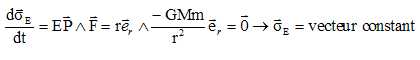La trajectoire est plane : ce plan passe par E et est peprendiculaire au moment cinétique. On suppose que la planète a un mouvement circulaire de rayon a, de période T et de vitesse vp.  Exprimer le rayon a puis la vitesse vp en fonction de G, T et M. La planète décrit la circonférence 2 p a en T seconde à la vitesse vP. 2 p a = vPT  ; 3ème loi de Kepler : T2/a3 = 4p2/(GM) ; a =  [GM T2 / (4p2)]1/3. vP = 2 p a /T = 2 p   [GM T2 / (4p2/)]1/3 /T = [GM 2p / T]1/3. On se place dans le cas du système Soleil-Terre. Calculer numériquement la masse du Soleil et la vitesse de la Terre sur son orbite. a = 1,50 1011 m ; T ~365,25 j =3,157 107 s. M =4p2 a3 /(T2G)=4*3,142 *(1,50 1011)3 /((3,157 107 )2*6,67 10-11)=2,00 1030 kg. vP =[6,67 10-11*2,00 1030*2*3,14  / (3,157 107 )]1/3= 2,98 104 m/s.   . . Référentiel barycentrique. Le mouvement du système étoile–-planète est décrit par rapport à un référentiel galiléen (Rgal). Soit I le centre d’inertie du système étoile-planète. Définir le référentiel barycentrique (R*). Est-il galiléen ? Référentiel barycentrique R* :  le repère d'espace centré en I est en translation par rapport à (Rgal). Or le système étoile-planète est isolé : R* est donc galiléen. Donner la relation entre les vecteurs-vitesse des centres E de l’'étoile et P de la planète dans le référentiel barycentrique. 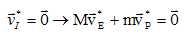Dans le cas où le mouvement de P est circulaire dans le référentiel barycentrique, décrire le mouvement de E dans ce référentiel. L'orbite de l'étoile est également circulaire de centre I. Il s'agit d'une homothésie de rapport -m/M par rapport àla planète. Que deviennent ces orbites quand m devient très petit devant M ? L'étoile est immobile ; la planète décrit un mouvement circulaire de rayon r. En déduire l’'expression approchée de vE* au premier ordre en m/M en fonction de G, T, M et m. D'une part vP*=vP =[GM 2p / T]1/3; d'autre part : vE*=m/M vP*. vE*=m/M[GM 2p / T]1/3 . . Des mesures donnent pour l’'étoile tBootis de la constellation du Bouvier : vitesse vE* = 470 m.s-1 ; période T = 3,31 jours ; masse M = 2,6×1030 kg. Calculer la masse de la planète en orbite autour de tBootis en supposant m<<M. L'’exprimer en prenant pour unité la masse de Jupiter. vE*=m/M[GM 2p / T]1/3  ; m = vE*M / [GM 2p / T]1/3 avec T = 3,31*24*3600 =2,86 105 s. m = 470*2,6 1030 / [6,67 10-11 *2,6 1030 *2*3,14 /(2,86 105)]1/3=7,83 1027 kg. MJ = 2,0 1027 kg ; m = 7,83 /2,0 = 3,9 MJ. .

menu