Diffusion
et spectroscopie Brillouin. Agrégation
2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Diffusion
Brillouin.
37.
On considère une onde acoustique de longueur d'onde l se
propageant
dans l'eau à la célérité v=1480 m/s. Cette onde peut être décrite en
terme de
particules, qu'on appelle des phonons.
Par
analogie avec le photon, définir la quantité de mouvement et l'énergie
d'un phonon. Les calculer pour une onde sonore de fréquence f = 1 kHz.
Commenter.
Le sens de la quantité de mouvement des phonons est le sens
de propagation de l'onde; sa norme est p = h / l.
L'énergie d'un phonon est e = hn.
l
= v / n
=1480 /1000 = 1,48 m ; p = 6,63 10-34 / 1,48
=4,48 10-34 kg m s-1.
e = 6,63 10-34
*1000 =6,63 10-31 J.
38. Quelle est la
longueur
d'onde minimum en dessous de laquelle la notion d'onde acoustique n'a
plus de sens ? En déduire l'ordre de grandeur de l'énergie maximum d'u
phonon. Comparer avec l'énergie typique d'un photon dans le
vide.
L'onde
acoustique a un sens dans les milieux continus. La longueur d'onde sera
donc bien supérieure à la distance moyenne entre deux molécules ( 10-10
m).
Pour une longueur d'onde égale à 10-9 m,
l'énergie e vaut environ 10-21 J, valeur 100
fois plus faible que l'énergie d'un photon du visible.
On donne le principe d'une expérience de diffusion Brillouin.
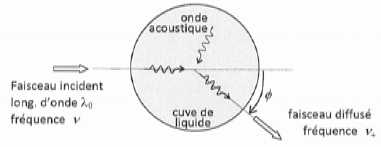
Un faisceau laser incident ( longueur d'onde dans le vide l0,
fréquence n
) éclaire une cuve cylindrique remplie de liquide. Les photons
incidents subissent des collisions avec les phonons acoustiques
correspondant aux fluctuations de densité du liquide. On détecte des
photons diffussés, c'est à dire la lumière diffusée ( fréquence n+,
dans une direction faisant un angle F
avec la direction du faisceau incident.On considère une collision dans
un liquide entre un photon incident, de quantité de mouvement P et un
phonon de quantité de mouvement p. Lors de cette collision, le phonon
disparaît et le photon diffusé acquiert une quantité de mouvement P+.
39. Ecrire
la conservation de
l'énergie lors de la collision. Que peut-on dire de la variation
relative de l'énergie du photon lors de cette collision ?
hn+
= hn
+ hf ( f : fréquence du phonon ).
L'énergie maximum d'un phonon est 10-21 J ;
énergie d'un photon du domaine visible ~10-19 J.
La variation relative de l'énergie du photon est donc faible.
40.
Que peut-on dire de la variation relative de la quantité de mouvement
du photon ? Ecrire la conservation de la quantité de mouvement et en
faire une représsentation graphique. En déduire que p ~ 2P sin(½F).
La quantité de mouvement et l'énergie d'un photon sont
proportionnelles. La
variation relative de la quantité de mouvement du photon est donc
faible.
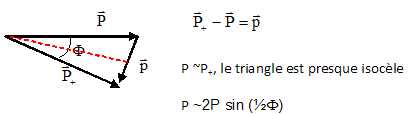
41.
On admettra que dans un milieu d'indice n, la quantité de mouvement du
photon incident s'écrit :
p = nh / l0.
Montrer que le décalage en fréquence dû à la difusion Brillouin est
donné par :
n+-n=2n /l0
v sin (½F).
Conservation de l'énergie : hn+=hn = hf
; n+
- n
= f = p v / h ;
p = 2Psin (½F)
=2 h n
/ c sin (½F) et
c = c0 / n.
n+
- n
= 2 n
v / c sin (½F) = 2 n
v n / c0 sin (½F) = 2 n
v n / c0 sin (½F) =
2n v / l0
sin
(½F).
42.
Pourquoi la diffusion Brillouin est-elle qualifiée d'inélastique ? Quel
est le décalage en fréquence s'il y a émission et non anihilation d'un
phonon au cours de la collision ?
Cette diffusion est dite "inélastique" car la fréquence du photon
incident est modifiée.
Qu'il y ait émission ou anihilation, les calculs sont les mêmes. Dans
le cas de l'anihilation le décalage est opposé.
43.
Calculer le décalage dans le cas de l'eau à T et P ambiantes pour l0
= 532 nm et pour F
= 90°, puis le décalage correspondant en longueur d'onde. La mise en
évidence de la diffusion Brillouin vous paraît-il possible
avec un
spectrophotomètre à réseau ?
n+
- n
=2*1,33*1480 / (532 10-9) sin 45 =5,23 109
Hz.
Décalage en longueur d'onde : Dl / l0
= Dn
/ n
;
l0-l=5,23 109 *532
10-9 / (5,64 1014) ~5 10-12 m
= 5 10-3 nm.
l0
/ ( l0-l)
~532 / 0,005 ~105. Un spectromètre à réseau ne
peut pas résoudre un tel décalage.
|
| .
. |
|
|
Principe
d'un interféromètre de Perot-Fabry.
Pour
analyser le décalage Brillouin, on utilise un interféromètre de
Perot-Fabry. Il est constitué de deux miroirs plans
parallèles,
semi-réfléchissants, de coefficient de réflexion élévé. On note e la
distance entre les miroirs, qui est de l'ordre du centimètre. On
assimile l'air à un milieu d'indice 1.
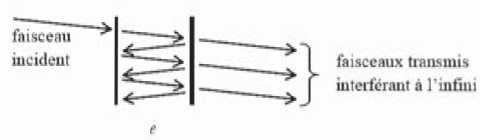
Par
commodité, les faisceaux sont représentés inclinés par rapport à la
normale aux miroirs, mais ils sont en réalité perpendiculaires aux
miroirs. On suppose tout d'abord que le faisceau incident est
parfaitement monochromatique de fréquence n.
44.
Calculer la différence de phase entre deux rayons sortants successifs.
Quel est l'ordre de grandeur de l'ordre d'interférence ?
La différence de phase entre deux rayons sortants successifs est 4p e
/ l
; il faut prendre en compte l'aller et retour dans la cavité.
L'ordre d'interférence est 2e/l
~0,02 / (532 10-9) ~4 104.
Pour
obtenir un spectre avec un Perrot-Fabry, on fait varier e sur une
distance de l'ordre du micromètre et on mesure l'intensité transmise It
en fonction de e.
45.
Pour quelles valeurs de e l'intensité transmise est-elle maximale ?
On admettra que, dès que e ne coïncide pas avec ces valeurs, It(e)
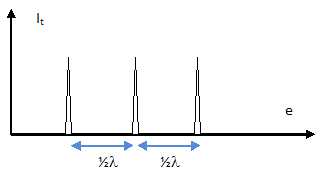
est très faible. Représenter, très schématiquement It(e)
en fonction de e.
Lorsque l'ordre d'interférence est un entier, It
est maximale.
2e/l = k
; e = pl/2
avec p un nombre entier.
On note e0 la distance pour laquelle l'ordre
d'interférence pour la fréquence n est
p, et e0+De
la distance pour laquelle l'ordre d'interférence est p+1. Le
faisceau incident est maintenant composé de deux raies de fréquences n et n' = n-dn ( dn
>0). Les deux raies sont très proches. On note e0+de
l'épaiseur pour laquelle l'ordre d'interférence est p pour la fréquence
n'.
46.
On suppose que de
<De.
Représenter It en fonction de e pour e0-De
< e <e0+De en
précisant pour chaque maximum la fréquence et l'ordre correspondant.
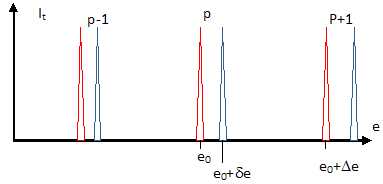
En
rouge, les pics correspondent à n.
47. Montrer que de /De = dn /
ISL où ISL=c/(2e0) est ce qu'on appelle
l'intervalle spectral libre de l'interféromètre.
e0 = ½pl ; e0+de = ½pl'
; de =½p(l' -l)
Diviser par De
=½l
: de
/ De =
p( l' /l -1).
Or ISL = c /(2e0) =pl / c
soit p = ISL c / l.
48. Que se
passe-t-il si |d n|
> ISL ? Conclure.
Il y a mélange des ordres pour les différentes fréquences.
Pour l'éviter, le domaine de fréquences doit rester inférieur à ISL.
|
|
|
|
On se place dans les
conditions expérimentales de la question 43. le faisceau diffusé
contient les raies de diffusion Brillouin n+
et n-,
mais il contient aussi la raie à la fréquence initiale n à
cause de la diffusion rayleigh qui résulte d'une diffusio élastique.
49.
On utilise un Perot-Fabry
dont l'ISL vaut 20 GHz. On fait l'expérience à pression et température
ambiante. Représenter l'allure de It(e) obtenue en sortie de
l'interféromètre en précisant pour chaque maximum la fréquence et
l'ordre d'interférence.
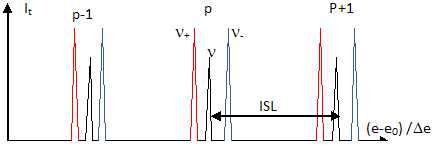
50. Pour des raisons
pratiques, on utilise un Perot-Fabry d'ISL 4 GHz. représenter à nouveau
l'allure It(e).
Les ordres se mélangent.
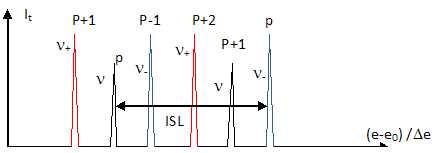
51.
La figure suivante représente deux spectres expérimentaux
obtenus
avec un perot-Fabry d'ISL = 4 GHz. Le spectre en trait continu est
obtenu à pression et température ambiante. Le second, légèrement décalé
est obtenu pour p = -26 MPa et à la même température.
- Pour chaque raie, indiquer la fréquence et l'ordre d'interférence.
- Vérifier que les positions des raies Brillouin à pression ambiante
sont cohérentes avec la valeur obtenue à la question 43.
- Estimer la variation de vitesse du son quand la pression passe de 0,1
à -26 MPa.
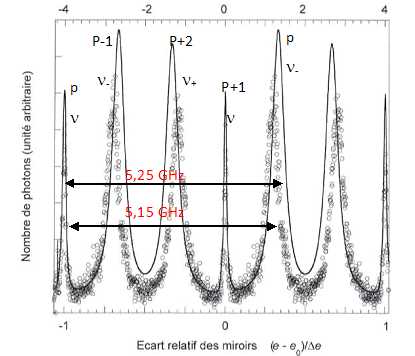
Le décalage Brillouin est proportionnel à la vitesse du son. -0,1 /
5,25 ~-0,02 (- 2 %).
Equation d'état de l'eau.
En plus de la vitesse du son v obtenue par diffusion Brillouin, on mesure également la masse volumique r
à la température T = 23,3°C. A cette température et sous pression
atmosphérique ( 0,101 Mpa), la masse volumique de l'eau vaut 997,5 kg m-3 et la vitesse du son v0 = 1493,5 m /s.
52. Pour des pressions positives et à T = 23,3°C, on trouve que v varie linéairement avec r. Sans mener à bien le calcul, expliquer comment on peut obtenir l'équation d'état P(r) à 23,3°C. La vitesse du son est donnée par : 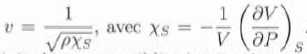
Vitesse : v = v0 +k(r-r0).
La compressibilité ( isotherme ou isentropique) s'écrit aussi :
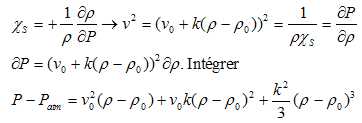
53.
En supposant que les relations de la question précédente peuvent
extrapolées à pression négative, calculer la vitesse du son pouri r = 985,2 kg m-3. k =3,558 m4 kg-1 s-1.
v = v0 + k(r-r0) =1493,5 +3,558(985,2 -997,5)= 1449,7 m/s.
54. la mesure directe donne v = 1449,9 m/s. Que pensez-vous de la validité de l'équation d'état évoquée à la question 52 ?
L'équation d'état est valide, les deux valeurs sont très proches. |
|
|
|