Equation différentielle, étude de fonction. Bts chmiste 2013.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice
1.
On considère deux réactions successives : 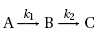
k1 et k2 désignent des
constantes de vitesse réelles distinctes, strictement positives et
vérifient k1 < k2.
A l’instant t (exprimé en minutes), on désigne par x(t ) et
y(t ) les concentrations exprimées en mol.L−1
respectivement des produits A et B. On admettra que x et y sont des
fonctions de variable t définies et dérivables sur l’intervalle [0 ;
+oo[.
Les lois cinétiques donnent les équations suivantes :
x′ = −k1x (1)
y′ = −k2y +k1x (2)
avec les conditions initiales : x(0) = a, y(0) = 0 où a est une
constante strictement positive.
Partie
I : Résolution
du système.
1.
Résoudre l’équation (1). En tenant compte de la condition initiale, en
déduire l’expression x(t ).
x (t)=A e-k1 t avec A une constante.
x
(0)=A =a ; x (t)=a e-k1 t.
2. Montrer que
l’équation (2) peut s’écrire sous la forme :
(E) : y′ +k2y = k1ae−k1
t.
y′
+k2y =k1x ; y′
+k2y =k1ae−k1 t.
3. a. Déterminer le
réel a
tel que la fonction g définie sur [0 ; +oo[ par g (t ) =ae−k1t
soit une solution particulière de l’équation différentielle (E).
g' = -k1ae−k1
t. Repport dans (E) :
-k1ae−k1
t+k2ae−k1t
=k1ae−k1 t.
-k1a+k2a =k1a.
a =k1a / (k2-k1).
b. Donner la
solution générale de l’équation différentielle (E).
Solution générale de y′
+k2y =0 : y = B e-k2t
avec B une constante.
Solution générale de (E) : y = B
e-k2t +ae−k1t.
4. Montrer que la
solution de l’équation différentielle (E) qui vérifie les conditions
initiales est la fonction y définie, pour t >0, par : y(t) = a ( e−k1t -e-k2t).
y
(0) =0 = B
+a
soit B = -a.
y
= -a e-k2t +ae−k1t
=a
(e−k1t
-e-k2t).
|
| .
. |
|
|
Partie II.
Etude de fonction
Soit la fonction f définie sur l’intervalle [0 ; +oo[ par : f (t ) = a
(e−0,5t −e−t ).
1.
Calculer, en justifiant, la limite de f (t ) lorsque t tend vers +oo.
Les deux termes en exponentielle tendent vers zéro lorsque t tend vers
l'infini. f(t) tend vers zéro si t devient très grand.
2. a.
Calculer la dérivée f ′ de la fonction f .
f ' = a(-0,5 e−0,5t +e−t ).
b. En déduire que la
fonction f admet un maximum en t0 = 2ln2.
f ' = 0 ; 0,5 e-0,5 t0
= e-t0 ; ln 0,5 -0,5 t0
= -t0 ; ln 0,5 =-ln2 =-0,5
t0 ; t0 = 2 ln2.
c. Montrer que
l’expression exacte du maximum de f est a / 4.
f(t0) =a
(e−ln2 −e−2ln2 ) = a(e+ln0,5
−e−ln4 )=a(e+ln0,5
−e+ln0,25 ) = a(0,5-0,25) = 0,25 a.
|
|
|
|
Partie III :
Détermination des différentes concentrations.
Dans cette partie, les constantes de vitesse k1
et k2 ont été choisies de telles sortes que la
concentration du produit B soit représentée par la fonction f étudiée
dans la partie II et la concentration du produit A, par une fonction h.
Les courbes C1 et C2 données
en annexe dans un repère orthogonal sont les représentations graphiques
respectives des fonctions f et h. (unités graphiques : 2 cm pour 1
minute sur l’axe des abscisses et 1 cm pour 0,01 mol.L−1
sur l’axe des ordonnées.)
1. En utilisant la
courbe C1, déterminer la valeur de la
concentration initiale du produit A notée a et exprimée en mol.L−1.
On laissera apparent les traits de construction.
2. On
désigne par z(t ) la concentration en mol.L−1 à
l’instant t du produit C (t exprimé en minutes).
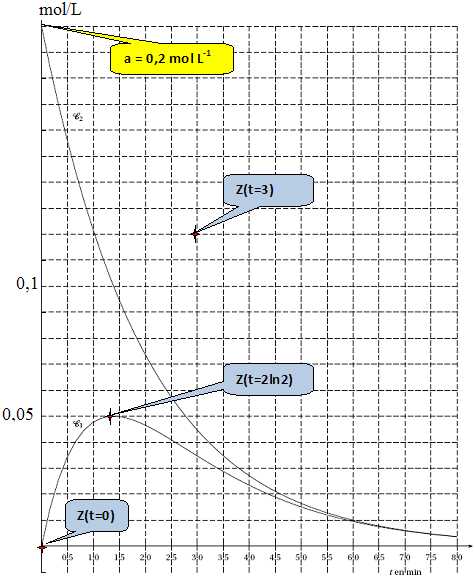
En utilisant le tracé de C1 et de C2
et sachant qu’à tout instant on a f (t )+ h(t )+ z(t ) = 0,2, tracer
sur l’annexe (à rendre avec la copie) les points de
coordonnées (t ,z(t )) pour t = 0, t = 2ln2 et t = 3.
t=0 : f (0 )+ h(0 )+ z(0 ) = 0,2 ; 0 +0,2 +z(0)=0,2 ; z(0)=0.
t = 2 ln2 : f(2ln2) =0,05 ; h(2ln2)=0,10 ; z(2ln2) =0,2-0,05-0,10 =
0,05.
t=3 : f(3) =0,035 ; h(3) =0,045 ; z(3)=0,2-0,035-0,045 = 0,12.
|
|