Probabilité,
test d'hypothèse. Bts chmiste 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Partie
I.
Soit X la variable aléatoire mesurant la durée de vie, en jours, d’un
atome radioactif d’iode 131 avant sa désintégration. X suit une loi
exponentielle de paramètre l=
0,087 (exprimé en jour−1).
1. a.
Montrer que P(X <= 6) = 1−e−0,522 et en
donner une valeur approchée arrondie à 0,01.
b.
Donner de même une valeur arrondie à 0,01 de P(X<=4).
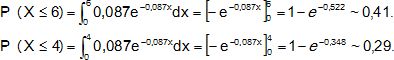
2. Soient
les évènements suivants concernant un atome d’iode 131 :
E : « sa durée de vie est d’au moins 6 jours ».
F : « sa durée de vie est d’au moins 4 jours ».
a. Que représente l’évènement E∩F ?
Déterminer sa probabilité.
La partie commune est " la durée de vie d'un atome d'iode 131 est d'au
moins 6 jours".
Probabilité q'un atome d'iode ne soit pas désintégré au bout de 6 jours :
1-0,41 = 0,59.
b.
Calculer la probabilité qu’un atome d’iode 131 ait une durée de vie
d’au moins 6 jours, sachant qu’il n’a pas été désintégré au bout de 4
jours.
Probabilité qu'un atome ne se soit pas désintégré au bout de 4 jours :1-0,29 = 0,71.
3.
Déterminer le réel t tel que P(X <= t ) = 0,5, on donnera la
valeur
exacte de t puis une valeur approchée arrondie à l’unité.
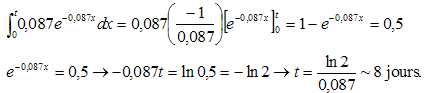
|
| .
. |
|
|
Partie II
Un laboratoire pharmaceutique commercialise des ampoules contenant de
l’iode 131.
Soit X la variable aléatoire qui, à chaque ampoule, associe la masse
d’iode 131, en mg, contenue dans un millilitre de solution.
On considère que X suit une loi normale demoyenne µ et d’écart-type s.
A :
Probabilités.
Cette
partie est un questionnaire à choix multiples. Pour chaque question,
une seule réponse est exacte. Indiquer sur la copie la lettre
correspondant à la réponse choisie. Aucune justification n’est
demandée. La réponse juste rapporte un point. Une réponse fausse ou
l’absence de réponse ne
rapporte ni n’enlève de point.
Pour les deux premières questions, on pose µ = 370 et s = 1,2.
1.
Une ampoule est commercialisable si la masse d’iode par mL est comprise
entre 368 et 372.
La probabilité arrondie à 0,001, qu’une ampoule soit non
commercialisable est égale à :
0,201 ; 0,096
( vrai) ; 0,052.
p(368
<= C <=372) = p(-1,67 <= (C-m)
/ s
<=1,667).
(C-m) / s suit
la loi normale centrée réduite : 2P(1,667)-1.
Les tables
donnent P(1,667) =0,952.
Probabilité pour qu'une ampoule
soit conforme : 2P(1,67)-1 =2*0,952-1 = 0,904.
Probabilité pour qu'une ampoule
soit non conforme 1-0,904 =0,096.
2.
Soit a le réel tel que P(370−a <= X <=370+a) =
0,95.
Une valeur arrondie à 0,01 de a est égale à : 2,35 ( vrai ); 2 ;
3,53.
Les tables donnent t = 1,96 ; a = s t =
1,2*1,96 =2,35.
|
|
|
|
Pour
les questions suivantes, on arrondit la probabilité p qu’une ampoule
soit non commercialisable àla valeur p = 0,1.
On
prélève au hasard un échantillon de 100 ampoules. La production est
assez importante pour que l’on assimile le prélèvement à un tirage avec
remise. On désigne par Y la variable aléatoire qui à tout échantillon
de 100 ampoules, associe le nombre d’ampoules non commercialisables.
Y suit la loi binomiale de paramètres n = 100 et p = 0,1 ( q =0,9).
3. Soit P1
la probabilité qu’il y ait exactement une ampoule non commercialisable
dans l’échantillon.
Une valeur arrondie à 10−6 de P1
est égale à : 2,95 10-4 ( vrai ) ; 0,1 ;
0,09.
P1
= C1100 p q99
=100*0,1*0,999 =2,95 10-4.
4.
Soit P2 la probabilité qu’il y ait au moins deux
ampoules non commercialisables dans l’échantillon.
Une valeur de P2 arrondie à 10−4
est égale à :0,01 ; 0,9997
(vrai); 0,9984.
P2 = 1-P(0)-P(1).
P(0) =C0100 p0
q100 =1*1*0,9100 =2,656 10-5.
P2 = 1-2,656 10-5-2,95 10-4
=0,9997.
5.
On considère que la loi Y est approchée par une loi de Poisson de
paramètre l.
Quelle valeur de l
semble être la plus appropriée ? 0,1 ; 10(vrai) ; 3,1,16.
l
= np =100*0,1 = 10.
B : Test
d’hypothèse.
Dans cette question, on suppose que s =
1,2.
Le
laboratoire indique que chaque ampoule contient 370 mg d’iode 131 par
mL.On se propose de construire un test bilatéral permettant d’accepter
ou de refuser cette affirmation, au risque 5%.
On désigne par µ la
moyenne en mg de la masse d’iode 131 contenue dans une ampoule. On
prélève au hasard un échantillon de n ampoules, la production étant
assez importante pour que l’on puisse assimiler ce prélèvement à un
tirage avec remise.
On prendra pour hypothèse nulle H0 : µ = 370 et
pour hypothèse alternative H1 : µ diffère de 370.
Soit Xn
la variable aléatoire qui à chaque échantillon de n ampoules prélevées
au hasard, associe la masse moyenne d’iode 131 par mL contenue dans ces
n ampoules. On admet que Xn suit la loi normale
demoyenne µ et d’écart-type s'
=1,2 /n½.
1.
Dans cette question, on prend n = 100.
X100 suit donc la loi normale de moyenne µ et
d’écart-type 0,12.
a. Déterminer
le réel h tel que, sous l’hypothèse H0, P(370−h
<= X<=370+h) = 0,95. On donnera une valeur approchée de h
arrondie à 10−3.
Les tables donnent t = 1,96. h = s't=
0,12*1,96 =0,2352 ~0,235.
b.
Énoncer la règle de décision permettant d’utiliser ce test.
Si la moyenne de l'échantillon appartient à l'intervalle [
369,765 ; 370,235], l'hypothèse H0 est valide,
sinon H1 est valide.
c.
Pour un échantillon de 100 ampoules prélevées au hasard, la masse
moyenne d’iode 131 par mL est x = 370,4.
Peut-on considérer, au risque 5%, que µ = 370 ?
370,4 n'appartient pas à [ 369,765 ; 370,235], H1
est valide ou bien la moyenne diffère de 370 mg.
2.
Le but de cette question est de trouver à partir de quelle valeur de
l’effectif n, on a P (370−0,2<= Xn moyen
<= 370+0,2)> 0,95 où Xn moyen
suit la loi normale de moyenne 370 et d’écart-type 1,2 /n½.
a.
Compléter, à l’aide de la calculatrice, le tableau donné en Annexe 1 à
rendre avec la copie.
b.
En déduire la valeur n cherchée.
| n
|
s'=1,2
/ n½ |
P
(370−0,2<= Xn moyen
<= 370+0,2) |
| 120 |
0,1095 |
0,9321 |
| 138 |
0,10215 |
0,9494 |
| 139 |
0,10178 |
0,9506 |
| 140 |
0,10142 |
0,9516 |
Xn moyen / s'
suit
la loi normale centrée réduite : 2P(0,2 /s' )-1 =2P(1,826)-1
Les tables
donnent P(1,826) =0,966.
2P(1,826)-1 =2*0,966-1
= 0,9321.
Xn moyen / s'
suit
la loi normale centrée réduite : 2P(0,2 /s' )-1 =2P(1,9566)-1
Les tables
donnent P(1,956) =0,9747.
2P(1,956)-1
=2*0,9747-1 = 0,9494.
Xn
moyen / s'
suit
la loi normale centrée réduite : 2P(0,2 /s' )-1 =2P(1,965)-1
Les tables
donnent P(1,965) =0,9753.
2P(1,965)-1
=2*0,9753-1 = 0,9506
Xn
moyen / s'
suit
la loi normale centrée réduite : 2P(0,2 /s' )-1 =2P(1,972)-1
Les tables
donnent P(1,972) =0,9758.
2P(1,972)-1
=2*0,9758-1 = 0,9516
|
|