Equation différentielle, étude de fonction. Bts chmiste 2015. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Partie 1 : équation différentielle. Soit le système (S)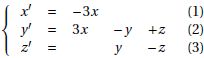 avec les conditions initiales x(0) = 1, y(0) = 0 et z(0) = 0. 1. a. Résoudre l’équation (1). b. En déduire x(t ) en tenant compte de la condition initiale x(0) = 1. x'+3x=0 ; x = A e-3t avec A une constante. x(t=0) = 1 = A ; x = e-3t. 2. a. En utilisant l’équation (3), exprimer y en fonction de z et z′ puis en déduire l’expression de y′ en fonction de z′′ et z′. y = z + z' ; y' = z' +z" b. En reportant dans l’équation (2) les résultats obtenus dans les questions 1. et 2. a., en déduire que z est solution de l’équation différentielle (E) : z′′ +2z′ = 3e−3t . z' +z" = 3e-3t -(z+z') +z ; z" +2z' = 3e-3t. 3. a. Résoudre l’équation différentielle z′′ +2z′ = 0. Equation caractéristique r2+2r=0 ; solution r = 0 et r =-2.  z= A +B e-2t avec A et B des constantes. b. Déterminer le réel a tel que la fonction g définie sur l’intervalle [0 ; +oo[ par g (t )= a e−3t soit une solution de l’équation (E). g' = -3ae-3t ; g" =9ae-3t. (E) s'écrit : 9ae-3t-6ae-3t = 3e−3t ; 3a=3 ; a=1. c. En déduire les solutions de (E). Solution générale de (E) = solution générale de z′′ +2z′ = 0 + solution particulière de (E). z = A +B e-2t +e−3t. 4. En utilisant l’équation (3), en déduire l’expression de y(t ) en fonction de A et B. y = z' + z = -2Be-2t-3e-3t +A+ B e-2t +e−3t. y = A -B e-2t -2e−3t. 5. En sachant que y(0) = 0 et z(0) = 0, déterminer les constantes A et B. En déduire z(t ) et y(t ). y(0) =A-B-2 =0 (1) ; z(0) =A+B+1=0 (2). (1)+(2) donne : 2A-1 =0 soit A = 0,5 ; par suite B = -1,5. y = 0,5 +1,5 e-2t -2e−3t ; z = 0,5 -1,5 e-2t +e−3t. . . Partie II On considère le schéma réactionnel : A→B⇆C impliquant les produits A, B et C. On suppose que les fonctions f , g et h qui à l’instant t > 0, exprimé en minute, associent les concentrations [A] de A, [B] de B et [C] de C, exprimées en mole par litre, sont respectivement les fonctions définies par : f (t ) = e−3t , g (t ) =0,5 +1,5 e-2t -2e−3t ; h(t) = 0,5 -1,5 e-2t +e−3t. Les trois courbes C1, C2, C3 tracées ci-dessous sont les représentations graphiques des fonctions f , g et h. 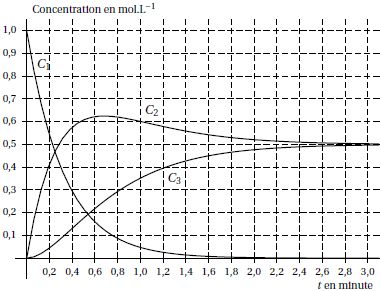1. a. Calculer f ′(t ). f '(t) = -3 e-3t. b. Déterminer le sens de variation de la fonction f . En déduire laquelle des trois courbes représente la fonction f . e-3t est toujours positif ; f '(t) est toujours négative et la fonction f est décroissante ( courbe C1). 2. a. Calculer l’instant t pour lequel les concentrations des produits A et C sont égales. On donnera une valeur exacte et une valeur de t arrondie à 0,01. f(t) = h(t) ; e−3t  = 0,5 -1,5 e-2t +e−3t. 0 = 0,5 -1,5 e-2t  ; e-2t   = 1 /3 ; ln (1/3) = -2t ; t = 0,5 ln 3 ~0,55 min. b. En déduire la courbe qui est la représentation graphique de la fonction h. C3 et C1 se coupent en un point d'abscisse t ~0,55. C3 est la représentation graphique de h(t). 3. a. Graphiquement, conjecturer la concentration finale du produit C. [C]finale = 0,5 mol/L. b. Retrouver le résultat par un calcul de limite. g (t ) =0,5 +1,5 e-2t -2e−3t. La limite de e-2t et e-3t est nulle si t est suffisamment grand ( supérieur à 3 min ).. La limite de g(t) est égale à 0,5 si le temps est supérieur à trois minutes. . .

menu