|
|
Partie
1.
On s’intéresse à la fonction donnant la pression (en kilo pascals)
exercés sur le fond du silo en fonction de la hauteur x (en mètres) de
grains contenus dans le silo. On admet que cette fonction vérifie
l’équation différentielle (E) : y′+0,175y = 8,365.
Dans cette équation, y désigne une fonction de la variable réelle x,
définie et dérivable sur l’intervalle [0; +oo[.
1.
Résoudre l’équation différentielle y′
y'+0,175y = 0.
y = A e-0,175 x avec A une
constante.
2.
Déterminer le réel a tel que la fonction g , définie sur [0; +oo[ par g
(x) = a, soit une solution particulière de l’équation (E).
g' = 0, repport dans (E) : 0,175 a = 8,365 ; a = 47,8.
3.
En déduire l’ensemble des solutions de l’équation différentielle (E).
y = A e-0,175 x +47,8.
4. Déterminer la
fonction p définie sur [0; +oo[ solution de l’équation différentielle
(E)
qui vérifie p(0) = 0.
p(0) = A+47,8 =0 ; A = -47,8.
p =
47,8 (1-e-0,175 x).
Partie
2.
On
considère la fonction f définie par [0; +oo[ par :
f (x) = 47,8(1−e−0,175x ).
Cette fonction f est celle qui, à toute hauteur x de grains contenus
dans le silo décrit dans la partie 1, associe la pression exercée sur
le fond de celui-ci.
On admet, pour l’étude théorique, que l’on peut remplir indéfiniment le
silo.
1. Étude théorique.
a.
Prévoir le sens de variation de f.
Lorsque l'on remplit de plus en plus le silo, la pression exercée par
le grain sur le fond augmente : f (x) est croissante.
b.
Justifier par le calcul le sens de variation de f .
f ' = 47,8*0,175 e-0,175 x.
e-0,175
x est positif, f ' est positive : f est croissante.
c. Démontrer que la
courbe représentative C de la fonction f admet une asymptote
horizontale D d’équation y = 47,8.
e-0,175 x
tend vers zéro si x devient grand.
f est alors équivalente à 47,8. La droite d'équation y = 47,8 est
asymptote.
À partir d’une certaines hauteur
de grains l,
on observe un effet de voûte à l’intérieur du silo, ce qui limite la
pression exercée sur le fond et provoque une augmentation de la
pression sur les parois latérales. Ce phénomène expliquele risque
d’éclatement d’un silo trop rempli. L’étude physique montre que l est
l’abscisse du point d’intersection de la tangente T à la courbe C au
point d’abscisse 0 et de son asymptote horizontale D.
|
|
|
2. La courbe
représentative C de la fonction f est fournie.
a.
Déterminer graphiquement, un encadrement de l par
deux entiers consécutifs.
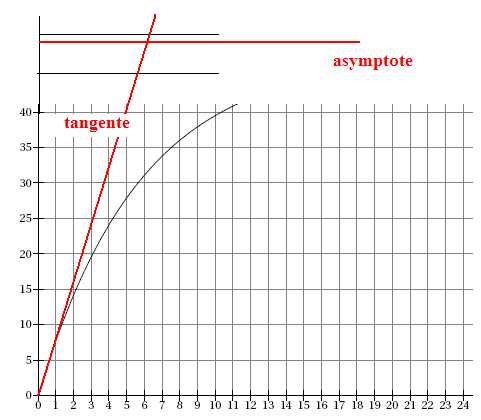
l
est compris entre 5 et
6.
b.
Déterminer une équation de la tangente T à C au point d’abscisse 0.
Coefficient directeur de la tangente : f '(0)=47,8*0,175 = 8,365.
y = 8,365 x.
c. En
déduire, par le calcul, une valeur approchée de l à 10−2.
y
= 8,365 l=
47,8 ; l =5,71.
|