Equation
différentielle, étude de fonction. Bts groupe D 2013.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Exercice
1.
Les bordures d’autoroute possèdent parfois des bassins de décantation
dont le rôle est de recueillir les eaux pluviales ruisselant sur
l’asphalte et les éléments polluants qu’elles peuvent drainer. À la
suite d’un accident de la circulation. un camion citerne déverse une
partie de son contenu sur la chaussée d’une autoroute. La
réglementation en vigueur impose l’isolation, par fermeture de vannes,
du bassin de décantation proche de l’accident de façon à ce que la
concentration en matières polluantes dans le bassin ne dépasse pas 15
μg/L. Cette concentration est de 1,3 μg/L au moment où les matières
polluantes provenant du camion-citerne commencent à se déverser dans le
bassin. Dans cet exercice, on cherche à prévoir au bout de
combien de temps la concentration en matières polluantes dans le bassin
atteindra 15 μg/L si on n’isole pas le bassin et à quel moment les
capteurs installés dans le bassin déclencheront la fermeture des vannes.
On mesure en minute le temps t écoulé à partir de l’instant où les
matières polluantes provenant du camion-citerne- commencent à se
déverser dans le bassin de décantation.
On admet que, tant que le bassin n’est pas isolé par fermeture des
vannes, la concentration
à l’instant t en matières polluantes dans le bassin, exprimée en μg/L
peut être modélisée par f (t ) où f est solution de l’équation
différentielle (E) : y′ +0,03y = 0,75.
On a donc f (0) = 1,3.
A. Résolution
sur l’intervalle [0 ; +oo[ de l’équation différentielle (E)
: y′ +0,03y = 0,75
1.
On considère l’équation différentielle
(E0) : y′ +0,03y = 0, où y est une fonction de
la variable t , définie et dérivable sur l’intervalle
[0 ; +oo], et y′ la fonction dérivée de la fonction y.
Déterminer les solutions de l’équation différentielle (E0)
sur l’intervalle [0 ; +oo].
y = A e-0,03 t avec A une
constante.
2.
Soit g la fonction définie sur l’intervalle [0 ; +oo] par g (t ) = a,
où a est une constante réelle.
Déterminer a pour que la fonction g soit une solution particulière de
l’équation différentielle (E).
g'(t)=0, repport dans (E) :
0+0,03a =0,75 ; a =25.
3. En déduire
l’ensemble des solutions de l’équation différentielle (E).
f(t) =25 +A e-0,03t.
4. Démontrer
que la solution f de l’équation différentielle (E) qui vérifie la
condition initiale f (0) = 1,3 est la fonction définie sur l’intervalle
[0 ; +oo] par : f (t ) = 25−23,7e−0,03t .
f(0) =25 +A =1,3 ; A = 1,3 -25 =
-23,7.
f (t ) = 25−23,7e−0,03t .
|
| .
. |
|
|
B. Étude de la fonction f.
f est définie sur l’intervalle [0 ; +oo] par : f (t )= 25−23,7e−0,03t .
On note C sa courbe représentative dans le plan muni d’un repère
orthogonal.
1. Déterminer la limite de la fonction quand t tend vers l'infini.
Le terme en exponentielle tend vers zéro quand t tend vers l'infini.
f(t) tend vers 25 quand t devient suffisamment grand.
2. On désigne par f ′ la fonction dérivée de la fonction f.
a. Calculer f ′(t ) pour tout t de l’intervalle [0 ; +oo].
f '(t) = 23,7*0,03 e−0,03t ; f '= 0,711 e−0,03t .
Expliquer le signe de f ′(t ) pour tout t de l’intervalle [0 ; +oo].
e−0,03t étant positive, f '(t) st positive sur [0 ; +oo].
3. Dresser le tableau de variations complet de la fonction f.
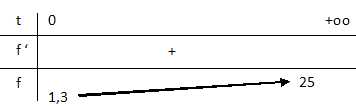
4. a. Recopier et compléter le tableau de valeurs ci-dessous. Arrondir
les résultats au dixième.
| t | 0 | 10 | 20 | 30 | 40 | 50 | 60 | | f(t) | 1,3 | 7,4 | 12,0 | 15,4 | 17,9 | 19,7 | 21,1 |
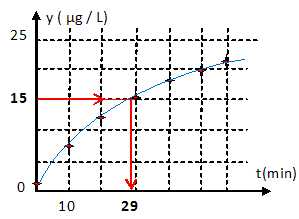
b. Tracer la courbe C.
|
|
|
|
C. Traitement de la problématique.
On
rappelle que f (t ) modélise la concentration (exprimée en μg/L) en
matières polluantes dans le bassin à l’instant t (exprimé en minute)
tant que le bassin n’est pas isolé par fermeture des vannes.
1.
Si le bassin n’était pas équipé d’un dispositif d’isolation par
fermeture de vannes, quelle serait la valeur autour de laquelle se
stabiliserait la concentration en matières polluantes ? Justifier.
f(t) tend vers 25 µg / L lorsque le temps devient sufisamment grand.
2. A l’aide de la courbe C déterminer graphiquement une valeur approchée à l’unité du temps t0 (exprimé en minute) au bout duquel la concentration
en
matières polluantes dans le bassin atteindrait 15 μg/L si le bassin
n’était pas isolé par fermeture de vannes. Expliquer la démarche.
t0= 29 min.
3. La concentration en matières polluantes dans le bassin est relevée par unvcapteur dont les mesures sont légèrement instables.
Pour
prendre en compte cette instabilité, on met en place un dispositif
associant la fermeture des vannes à l’instant t (t > 2) à la valeur
moyenne de la concentration en matières polluantes mesurée par le
capteur entre les instants t −2 et t .
La fermeture des vannes est déclenchée lorsque cette valeur moyenne atteint 14 μg/L.
La valeur moyenne de la concentration (exprimée en μg/L) en matières polluantes entre les instants t −2 et t est modélisée par :
V(t) = ½F(t)-F(t-2) où F est une primitive de la fonction f
a. Donner une primitive F de la fonction f sur l’intervalle [0 ; +oo].
f (t )= 25−23,7e−0,03t.
F(t) = 25 t + 23,7 / 0,03 e−0,03t.
F(t) = 25 t +790e−0,03t.
b. Calculer V (t ) et vérifier que : V (t ) = 25+ Ae−0,03t avec A = −24,4.
F(t-2) = 25 (t-2) +790e−0,03(t-2) =25 (t-2) +790e−0,03t e0,03*2 =25 (t-2) +838,85e−0,03t.
F(t)-F(t-2) =50 -48,85 e−0,03t.
V(t) = ½(F(t)-F(t-2)) =25 -24,4e−0,03t.
c. Résoudre l’équation : 25−24,4e−0,03t = 14. Donner une valeur approchée au dixième de la solution T de cette équation.
e−0,03T =(25-14) / 24,4 = 0,4508.
-0,03 T = ln 0,4508 = -0,7967 ; T = 0,7967 /0,03 =26,55 ~26,6 min.
d. Que représente T dans le contexte de l’exercice ?
La fermeture des vannes est déclenchée à la date T.
|
|