Equation différentielle, étude d'une fonction. Bts maths groupe C 2015. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Une étude est menée concernant la suspension de véhicules. On considère que la suspension d’un véhicule est constituée, au niveau de chaque roue, d’un ressort et d’un amortisseur (voir figure). Pour un véhicule donné, le déplacement vertical des suspensions, en cas de sollicitation, dépend du coefficient d’amortissement l. En laboratoire, on étudie le comportement de différents véhicules quand on les écarte de leur position d’équilibre. Le chronomètre est déclenché au moment où le ressort est étiré de 10 cm.  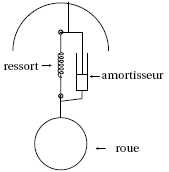A :  Différents cas d'amortisseurs. 1. Comparaison de deux amortisseurs On modélise le déplacement vertical du centre d’inertie du véhicule par rapport à sa position d’équilibre (exprimé en centimètre), en fonction du temps (exprimé en seconde) par la fonction f dont la représentation graphique dans un repère orthogonal est donnée ci-dessous, pour deux valeurs différentes l1 et l2 du coefficient d’amortissement. Lorsque t représente un temps exprimé en seconde, f (t ) représente le déplacement vertical du centre d’inertie à l’instant t 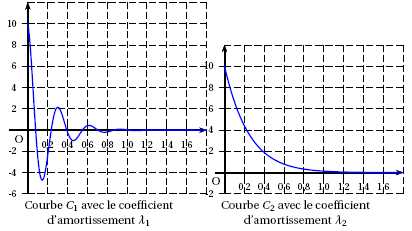. a. Dans chacun des deux cas, décrire le comportement du véhicule à l’aide du graphique. b. Quel coefficient d’amortissement est-il plus intéressant d’avoir ? Expliquer. Courbe C1 : le mouvement est oscillatoire amorti, ce qui est désagréable pour les passagers. Courbe C2 : le mouvement est apériodique. Le confort est meilleur. 2. Dans cette question, on s’intéresse à un autre amortisseur. Pour la valeur du coefficient d’amortissement qui lui correspond, le véhicule est ramené à sa position d’équilibre en un temps minimum et sans oscillation. On parle alors d’amortissement critique. On admet que la fonction donnant le déplacement vertical du centre d’inertie du véhicule par rapport à sa position d’équilibre, en fonction du temps, est alors solution de l’équation différentielle (E) : y′′ +40y′ +400y = 0. où y désigne une fonction de la variable t , définie et deux fois dérivable sur l’intervalle [0 ; +oo[. a. Résoudre l’équation différentielle (E) : Equation caractéristique : r2 + 40 r+400 = 0 ; D = 402-4*400 = 0. r = -40 / 2 = -20 ; y = (At+B) e-20t avec A et B des constantes. b. Déterminer la fonction f , solution de l’équation différentielle (E), qui vérifie f (0) = 10 et f ′(0) = 0. f(0) = B = 10 ;  f '(t)=A e-20t -20(At+B)e-20t  ; f '(0) = A-20 B = 10 ; A = 200. f = (200t+10) e-20t . . . On considère la fonction f dérivable sur [0 ; +oo[, définie par : f (t ) = (200t +10)e−20t dont la courbe représentative C dans un repère orthogonal est donnée. 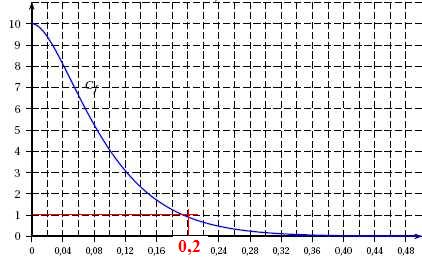1. Par lecture graphique, déterminer les variations de f ainsi que les coefficients directeurs des tangentes à la courbe aux points d’abscisses respectives 0 et 0,4. La fonction est décroissante sur [0 ; +oo[. A t=0, la tangente est horizontale,coefficient directeur  : 0 A t =0,4, la tangente est horizontale, coeficient directeur  : 0. 2. a. Démontrer que pour tout t de [0 ; +oo[ on a f ′(t )= −4000t e−20t . On pose u = 200t+10 et v = e-20t. u' = 200 ; v' = -20(200 t+10)e-20t. f '(t) = u'v+v'u = 200 e-20t -4000te-20t-200e-20t =−4000 t e−20t . b. Indiquer, en justifiant, si les trois résultats obtenus graphiquement à la question 1. sont confirmés. sur [0 ; +oo[,e−20t >0 ;  te−20t >0 ; f '(t) <0, fonction décroissante. f '0) =0, tangente horizontale. f '(0,4) = -0,53, la tangente est pratiquement horizontale. 3. On admet que cette fonction f est celle qui donne le déplacement vertical par rapport à sa position d’équilibre, en centimètre, du centre d’inertie du véhicule équipé de l’amortisseur étudié à la question 2. Partie 1, en fonction du temps, exprimé en seconde. Déterminer graphiquement au bout de combien de temps le déplacement vertical du centre d’inertie du véhicule par rapport à sa position d’équilibre sera inférieure au dixième du déplacement initial. A t > 0,20 s,  le déplacement du centre d'inertie est inférieur à 1 cm. 4  Un logiciel de calcul formel  donne en intégrant f(t): F = (−exp(−20∗ t ))∗(10∗ t +1). a. Que représente la fonction F définie sur [0 ; +oo[ par F(t ) = −(10t+1)e−20t relativement à la fonction f ? F est une primitive de f(t). b. En déduire le déplacement moyen du centre d’inertie du véhicule entre les instants t = 0 s et t = 0,4 s. Déplacement moyen ymoy =[F(0,4)-F(0) ] / (0,4-0). F(0,4) = - (10*0,4 +1)e-8 = -0,00168. F(0) = -1. ymoy =(-0,00168+1) / 0,4 ~2,5 cm. ans .

menu