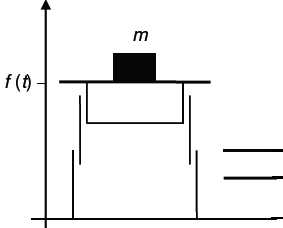
Equation différentielle, étude d'une fonction. Bts maths groupe B 2015. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . Sur une chaîne de montage, une pièce de 10 kg est située sur un plateau. On note f (t) la cote (en mètres) du plateau à l’instant t (en secondes), calculée par rapport au sol. On suppose que f est une fonction de la variable réelle t définie et deux fois dérivable sur [0, + oo[. L’objectif de l’exercice est d’étudier f afin de réaliser correctement le transfert de la pièce sur un tapis roulant.  A :  Résolution d'un équation différentielle. On considère l’équation différentielle (E) : y " + 5 y ' + 4y = 10 , où y est une fonction de la variable réelle x, définie et deux fois dérivable sur [0, + oo[, y ' la fonction dérivée de y et y '' sa fonction dérivée seconde. 1° a) Résoudre dans R l’équation r 2 + 5 r + 4 = 0. Discriminant D = 52-4*4 = 9 ; D½ = ±3. r1 = (-5+3) / 2 = -1 ; r2 = (-5-3) / 2 = -4. b) En déduire les solutions définies sur R de l’équation différentielle (E0) : y " + 5 y ' + 4y = 0. y = A e-t +B e-4t avec A et B des constantes. 2° Un logiciel de calcul formel résout ci-dessous l’équation différentielle (E). y = A exp-t +B e-4t +2,5. L’étude du système mécanique montre que f est la solution de l’équation différentielle (E) vérifiant les conditions initiales f (0) = 5 et f '(0) = – 1. En utilisant le résultat du logiciel, qu’on ne demande pas de démontrer, déterminer une expression de f (t) en fonction de t. f(0) = A+B+2,5 = 5 ; A+B = 2,5 (1). f ' = -Aexp-t -4B e-4t  ; f '(0) = -A-4B = -1 ; A+4B = 1 (2) (2)-(1) donne : 3B = -1,5 ;B = -0,5. Par suite A = 3. f(t) = 3 e-t -0,5 e-4t +2,5. B. Etude d'une fonction. 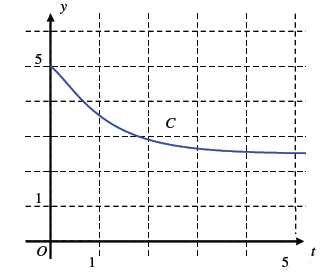La courbe C ci-dessous est la représentation graphique, dans un repère orthogonal  de la fonction f définie sur [0, + oo[ par f (t) = 3 e– t – 0,5 e– 4 t + 2,5 . 2. Etude d'une fonction. 1° a) Conjecturer le sens de variation de la fonction f sur l’intervalle [0, +oo[. Le graphique indique que f est décroissante sur [0 ; +oo[. b) Un logiciel de calcul formel donne ci-dessous une expression de la dérivée de f. f '(t) = -e-4t(3e3t-2). On admet que, pour tout réel t de l’intervalle [0, + oo[, 3 e 3 t – 2 > 0. En utilisant, sans le démontrer, le résultat du logiciel, justifier la conjecture de la question 1° a). e-4t est positif ; -e-4t est négatif ; f '(t) est négatif sur [0, + oo[. f(t) est décroissante sur cet intervalle. . . 2° Le logiciel de calcul formel permet d’obtenir le développement limité de la fonction f, à l’ordre 2, au voisinage de 0.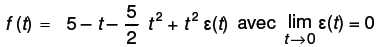 b) Donner une équation de la tangente T à la courbe C au point d’abscisse 0.  y = 5-t. c) Étudier la position relative de la courbe C et de la tangente T au voisinage du point d’abscisse 0. Etude du signe de f(t)-y = -2,5 t2 est négatif. T est au dessus de C. 3° a) Déterminer la limite de f(t) lorsque t tend vers l'infini. e-t et e-4t tendent vers zéro lorsque t tend vers l'infini. f(t) tend vers 2,5 lorsque t tend vers l'infini.. b) Interpréter graphiquement la limite obtenue à la question 3° a) en termes d’asymptote. La droite d'équation y =2,5 est asymptote à la courbe C.  C : Transfert de la pièce sur le tapis roulant. On admet la modélisation selon laquelle la cote f (t) (en mètres) du plateau à l’instant t (en secondes), calculée par rapport au sol, est donnée par la fonction f définie et représentée dans la partie B. La partie supérieure du tapis roulant est située à 2,5 mètres du sol. La pièce peut être transférée dès qu’elle se situe à un centimètre du tapis roulant. 1° A partir de quel instant t0 la pièce peut-elle être transférée sur le tapis roulant ? Pour cette question, on attend une valeur approchée de t0 arrondie au dixième par excès, obtenue à l’aide de la calculatrice, en expliquant la méthode suivie. La pièce peut être transférée sur le tapis si f(t) = 2,51 soit 3 e-t -0,5 e-4t = 0,01. Pour t > 4 s, le terme -0,5 e-4t est négligeable devant 3 e-t ; e-t ~0,01 / 3 soit et ~300 ; t =5,7 s. 2° L’algorithme suivant affiche les bornes d’un encadrement de t0. Variables : a, b, m Initialisation : a prend la valeur 5 b prend la valeur 6 Traitement : Tant que b – a > 0,1 m prend la valeur (a+b) / 2 Si f (m) > 2,51 alors a prend la valeur m Sinon b prend la valeur m Fin de Si Fin de Tant que Sortie : Afficher a et b a) Faire tourner cet algorithme « à la main » sur trois étapes en complétant le tableau cidessous. Etape 1 Etape 2 Etape 3 a 5 5,5 5,5 b 6 6 5,75 b-a 1 0,5 0,25 m (5+6) / 2 = 5,5 5,75 5,625 b) Que peut-on dire de l’amplitude de l’encadrement de t0 fourni par cet algorithme ? L'amplitude de l'encadrement au bout de 3 étapes est 0,25, valeur supérieure à la condition d'arrêt de la boucle. ans .

menu