Etude
du fonctionnement d'une pompe à chaleur.
Bts FEE 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Étude du
fonctionnement de la pompe à chaleur (8 points)
Cette pompe à chaleur fonctionne avec le fluide frigorigène R134a. Ce
dernier décrit le cycle
thermodynamique dont l'allure est donnée.
Son débit massique est constant et vaut qm = 0,87 kg.min–1.
Au point A, le fluide est sous forme de vapeur saturée à la pression pA
= 3,5 bar et à la température qA = 5,0 °C. Il subit alors une compression adiabatique jusqu'à la pression pB =
11,6 bar et atteint la température qB (point B).
Puis il passe dans l'échangeur où la vapeur se refroidit (point B’),
puis se condense en cédant de
la chaleur à l'eau sanitaire. À la sortie du condenseur (point C), le
fluide est entièrement liquide.
Le fluide subit ensuite une détente isenthalpique, à la sortie du
détendeur, le fluide est sous forme
d’un mélange liquide-vapeur (point D).
Enfin, le liquide restant s'évapore grâce à la chaleur reçue par l'air
aspiré et revient dans l'état de
vapeur saturée (point A).
A. Diagramme enthalpique du cycle.
Toutes les transformations sont supposées réversibles.
1. À quelle étape correspond la transformation subie par le fluide entre les états A et B ?
Étape 3 : le fluide frigorigène est comprimé grâce au compresseur afin d’augmenter sa température et sa pression.
2. Parmi les termes suivants, choisir celui qui indique la nature de la transformation entre les états
B et C : isotherme – isochore – isobare – adiabatique – isentropique – isenthalpique.
La transformation B --> C s'effectue à pression constante : isobare.
3.
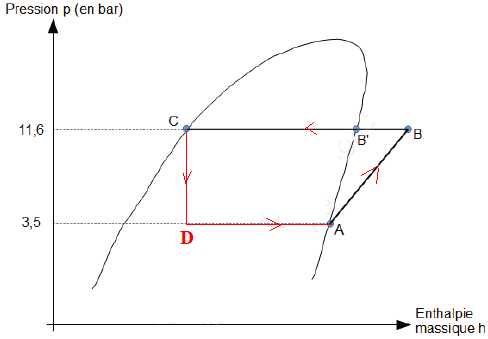
Terminer le tracé du cycle en indiquant le point D (état du fluide à la
sortie du détendeur) et en orientant chaque transformation.
|
| .
. |
|
|
B. Grandeurs caractéristiques du fluide
Le fluide frigorigène R134a, nommé aussi 1,1,1,2-tétrafluoroéthane, a pour formule brute C2H2F4.
Il se comporte comme un gaz parfait de constante massique r, de coefficient adiabatique g et
de capacité thermique massique à pression constante cP = 660 J.kg–1.K–1.
Données :
- masses molaires atomiques M en g.mol–1 : H : 1,0 ; C : 12,0 ; F : 19,0 ;
- constante molaire caractéristique des gaz parfaits : R = 8,31 J.mol–1.K–1 ;
- relations entre les capacités thermiques massiques à pression constante cP et à volume
constant cV : γ = cP / cV ; r = cP – cV.
1. Montrer que la constante massique du gaz parfait R134a vaut r = 81,5 J.kg–1.K–1.
M(C2H2F4)=2*12+2+4*19 = 102 g/mol.
r =R /M = = 8,31 / 0,102= 81,5 J.kg–1.K–1.
2. Exprimer le coefficient adiabatique g en fonction des grandeurs r et cP, puis calculer sa valeur.
cV =cP / g ; r =cP – cV = cP(1-1/g) ;
r / cP = 1-1/g ; 1/g =1-r / cP =(cP-r) / cP ; g = cP /(cP-r) =660/(660-81,5)=1,14.
|
|
|
|
C. Étude du cycle thermodynamique.
1. On s’intéresse à la compression du fluide entre les états A et B.
a) À partir de la relation de Laplace P1-g Tg = constante, valable pour une transformation adiabatique réversible d’un gaz parfait, exprimer la température TB en fonction de TA, pA, pB et g.
PA1-g TAg =PB1-g TBg ; TBg = PA1-g TAg /PB1-g ;
TB =TA ( PA / PB) (1-g)/g.
b) Faire l’application numérique avec qA = 5,0 °C, pA = 3,5 bar, pB =11,6 bar et g = 1,14.
TB =(273+5)(3,5 / 11,6) -0,14 /1,14 =322 K.
Pour la suite de l’exercice, on prendra TB = 322 K.
2.
À l’aide du premier principe de la thermodynamique pour un fluide en
écoulement, exprimer le travail massique de transvasement du
compresseur wcomp, en fonction des températures TA et TB puis vérifier que wcomp = 29,0 kJ.kg–1.
DhAB= wcomp +QAB =cP(TB-TA) avec QAB =0 ( adiabatique).
wcomp =cP(TB-TA) =660(322-278)=2,9 104 J kg-1 = 29 kJ kg-1.
3. On rappelle que la puissance du compresseur est égale au produit du travail massique de l’appareil par le débit massique qm du fluide.
Calculer la valeur, en watts, de la puissance du compresseur Pcomp.
Pcomp = wcomp qm =2,9 104 *0,87 /60 =421 W.
4. On note Pth, la puissance thermique cédée par le fluide à l’eau sanitaire dans le condenseur.
a) Rappeler l’expression du coefficient de performance, noté COP, de cette pompe à chaleur en fonction de Pcomp et Pth.
COP = puissance récupérée à la source chaude / travail investi = Pth / Pcomp .
b) Le constructeur indique un COP de 3,6. Calculer alors la valeur de Pth.
Pth = COP Pcomp =3,6 *421 = 1,52 103 W.
|
|
|
|