Impact
acoustique d'une station d'épuration ; étude d'un bassin d'orage.
Bts enveloppe du bâtiment 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Partie 1 : Impact acoustique
d’une station d’épuration (7 points).
On étudie ici l’impact acoustique en période nocturne d’une station
d’épuration sur son voisinage.
En effet, une station d’épuration fonctionnant 24 heures sur 24, il est
important d’évaluer son impact sonore sur l’environnement. De tous les
systèmes en fonctionnement dans une telle installation, il est
communément admis que les surpresseurs sont les principaux responsables
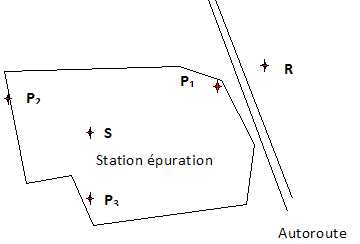
des nuisances sonores. Ils sont localisés au point S du plan de la
station donné.
Afin de quantifier ces nuisances sonores un technicien a effectué des
relevés du niveau de bruit
aux points P1, P2 et P3
comme indiqué sur le plan de la station donné.
Caractéristique du
bruit résiduel nocturne sans les surpresseurs.
| Fréquence
médiane (Hz) |
63 |
125 |
250 |
500 |
1000 |
2000 |
4000 |
Niveau
global ( dB(A) |
| Point
P1 |
46,0 |
41,0 |
41,0 |
40,0 |
36,0 |
27,0 |
17,0 |
40,7 |
| Point
P2 |
42,0 |
41,0 |
46,0 |
45,0 |
37,0 |
29,0 |
21,0 |
44,3 |
| Point
P3 |
41,0 |
40,0 |
45,0 |
43,0 |
36,0 |
29,0 |
20,0 |
42,9 |
1.1. Pourquoi
pondère-t-on les niveaux acoustiques en dB(A) ?
La sensibilité de l'oreille, c'est à dire sa capacité à entendre, ne
sera pas la même selon la hauteur du son parvenant à l'oreille de
l'auditeur. D'autre part, un son émis par une source avec un certain
niveau sonore ne sera pas perçu par l'oreille avec ce même niveau
sonore.
1.2. En calculant le
niveau pondéré pour chaque bande d’octave au point P1,
remplir entièrement le tableau suivant.
| Fréquence
médiane (Hz) |
63 |
125 |
250 |
500 |
1000 |
2000 |
4000 |
Niveau
global ( dB(A) |
| Point
P1 |
46,0 |
41,0 |
41,0 |
40,0 |
36,0 |
27,0 |
17,0 |
|
| Pondération
( dB(A)) |
-26,2 |
-16,1 |
-8,6 |
-3,2 |
0 |
1,2 |
1,0 |
|
| Niveau
sonore pondéré dB(A) |
19,8 |
24,9 |
32,4 |
36,8 |
36 |
28,2 |
18 |
40,7 |
1.3. Montrer par un calcul
que le niveau de bruit global Ltot= S 10Li/10 ,
avec Li, le niveau sonore à la fréquence i au
point Pi, est bien environ égal à 41 dB.
Les
intensités acoustiques de chaque bande d'octave s'ajoutent :
Itotal = S I où i = 1,2,3,…,6.
Itotal
/ IP0 = S
I
/ I0 ; I / I0 = 10Li/10.
Itotal
/ I0 = S 10Li/10.
Ltotal =
10 log( Itotal / I0
)=10
log S 10Li/10.
S 10Li/10=101,98
+102,49+103,24+103,68+103,6+102,82+101,87=95,5+309
+1738
+4786+3981 +661 +74 =
11644.
Ltotal
=10 log(11644)=40,79
dB.
|
| .
. |
|
|
Niveau de bruit de
la station d'épuration.
1.4 Calculer les
émergences aux trois points étudiés.
| Point |
Niveau de
bruit ambiant dB(A) |
Emergence
(dB(A)) ( bruit engendré par la station) |
| Equipement
en fonctionnement |
Equipement
à l'arrêt |
| P1 |
47 |
41 |
6 |
| P2 |
48 |
45 |
3 |
| P3 |
48 |
43 |
5 |
1.5 La station
d’épuration respecte-t-elle les normes établies en période nocturne pour
chacun des trois points ? Justifier.
Au points P1 l'émergence est supérieure aux
normes admissibles de jour comme de nuit. La station ne
respecte pas les normes.
Au points P3 l'émergence
est supérieure aux normes admissibles de nuit. La station ne
respecte pas les normes concernant la période 22 h à 7 h.
Au points P2 l'émergence
est inférieure ou égale aux normes admissibles de nuit comme
de jour. La station respecte les normes.
1.6 L’emplacement
des surpresseurs noté (S) est situé à 50 m du point 1, noté P1.
Le riverain, noté R, est à 10 m de P1. Les
points S, P1 et R sont alignés.
Déterminer le niveau sonore Ltot (R) chez le
riverain si Ltot(P1) = 47 dB(A).
Ltot
(R) =Ltot(P1) +20 log(rP1
/rR)
Ltot (R) est le niveau sonore
global en dB(A) à la distance rR de la source
sonore et Ltot(P1) est le niveau sonore en dB(A) à
la distance rP1 de la source.
Ltot (R) =47 +20 log(50
/60)=47-1,6 =45,4 dB(A).
1.7
Sachant que le niveau résiduel au niveau du riverain est de 39 dB, le
niveau sonore est-il conforme aux normes établies ?
Emergence en R due au surpresseurs :
45,4-39 = 6,4 dB, valeur supérieure aux normes.
|
|
|
|
Étude d’un bassin d’orage (6 points)
Les
dimensions intérieures du bassin d’orage cylindrique auquel on
s’intéresse sont données: D = 35 m ; H = 12,5 m. Ce bassin d’orage est
alimenté par une galerie cylindrique de 315 m de long et de 2,20 m de
diamètre.
2.1 Montrer que le volume de stockage du bassin d’orage est d’environ 12000 m3.
V = pD2/4 H =3,14*352/4*12,5=1,2 104 m3.
2.2 Le bassin d’orage est vidangé par pompage. Le système de pompage a un débit de D = 300 L/s.
Calculer le temps T de vidange du bassin.
T= V / D = 1,2 104 /0,3 =4,0 104 s ~11 h 8 min.
La canalisation de vidange a une section de s = 0,38 m2. Vérifier que la vitesse v de l’eau dans la canalisation est d’environ 0,79 m.s-1.
D = 0,3 m3 /s ; v = D / s = 0,3 / 0,38 = 0,79 m / s.
2.3
Dans un document technique, un ingénieur écrit que le fond du bassin
d’orage est étudié pour supporter « 13 tonnes d’eau par m2 » maximum (sans tenir compte de la pression atmosphérique).
On suppose que le bassin est complètement rempli.
Données : accélération de la pesanteur g = 9,8 m.s-2.
Masse volumique des eaux pluviales r = 1000 kg.m-3.
- Expliciter en termes de pression ce qu’a voulu dire cet ingénieur.
Poids de 13 tonnes d'eau : 13 000*9,81 = 1,18 105 ~1,2 105 N par m2 soit une pression due à l'eau de 1,2 105 Pa = 1,2 bar.
- Calculer la pression due à l’eau au fond du bassin, sans tenir compte de l’indication de l’ingénieur et conclure.
p = rgH =1000*9,81*12,5 =1,22 105 ~1,2 105 Pa.
Le fond du bassin supporte la pression de l’eau.
|
|
|
|