Analyse par
fluorescence X. Bts chimiste 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Production de rayons X à l’aide
d’un tube scellé à rayons X.
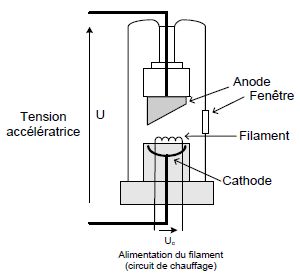
Dans une enceinte sous vide, les électrons émis par un filament chauffé
sont accélérés d’une cathode vers une anode sous l’action d’une haute
tension U. Ils sont alors freinés par les atomes de la cible (anode), ce qui provoque un
rayonnement continu de freinage dans le domaine des rayons X. On rappelle que les
rayons X sont des rayonnements de longueur d’onde comprise entre environ 10-1 nm
et 10-3 nm.
Les
électrons peuvent également exciter les atomes de la cible ; la
lacune électronique provoquée est suivie d’une réorganisation
quasi-instantanée du cortège électronique qui se traduit par l’émission
de photons X de fluorescence. Le spectre « sortant » du tube est donc
la superposition du rayonnement
de freinage et de raies de fluorescence X caractéristiques de la cible.
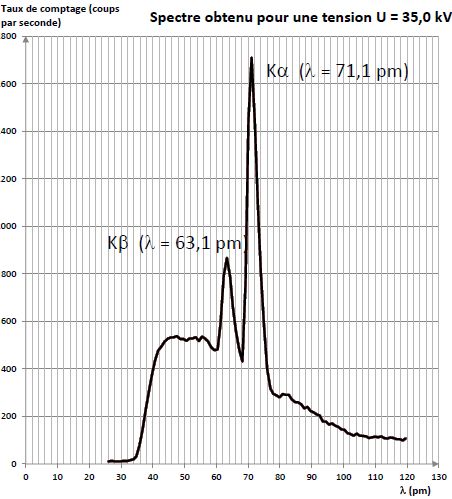
On donne le spectre obtenu pour une tension U = 35,0 kV.
Dans tout le problème, les effets de la pesanteur seront considérés
comme négligeables.
Schéma d’un tube à rayons X :
Influence de la haute tension U sur l’énergie maximale des photons X produits.
Établir l’expression de l’énergie cinétique d’un électron arrivant sur
l’anode en fonction de la charge élémentaire e et de la tension
accélératrice U (on supposera que l’électron part de la cathode sans
vitesse initiale).
L'électron n'est soumis qu'à la force électrique. Le travail de celle-ci est moteur et vaut eU.
Variation de l'énergie cinétique de l'électron entre anode et cathode : ½mv2-0.
Par suite : ½mv2 = eU.
L’énergie maximale des photons X du rayonnement de freinage se calcule
en considérant que l’énergie cinétique de l’électron arrivant dans
l’anode est intégralement convertie en énergie rayonnée. Déterminer en
joule et en électron-volt cette énergie maximale pour U = 35,0 kV.
Emax = eU = 1,60 10-19 *35,0 103 =5,60 10-15 J = 35,0 keV.
Montrer que la longueur d’onde minimale lmin des photons X produits s’écrit : lmin = hc / (eU).
lmin = hc / Emax = hc / (eU).
Vérifier,
que dans les conditions de l’expérience, la longueur d’onde minimale
des photons produits appartient bien au domaine des rayons X.
lmin = 6,63 10-34 *3,00 108 /(5,60 10-15)=3,55 10-11 m =3,55 10-2 nm.
Les
rayons X sont des rayonnements de longueur d’onde comprise entre environ 10-1 nm
et 10-3 nm.
|
| .
. |
|
|
Détermination expérimentale de la constante de Planck.
Pour différentes valeurs de la tension accélératrice U, on mesure la longueur d’onde minimale lmin des rayons X émis.
Afin de vérifier que les valeurs de lmin sont inversement proportionnelles à celles de la tension accélératrice U, on trace la courbe lmin = f (1/U) que l’on modélise grâce à une régression linéaire dont les résultats sont indiqués sur le graphe ci-dessous :
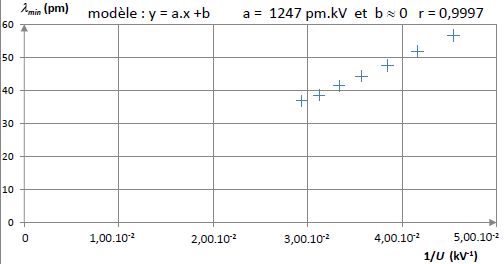
Quelles informations présentes sur ce graphe permettent de vérifier que les valeurs de lmin sont bien inversement proportionnelles à celles de U ?
En joignant les points on obtient une droite passant par l'origine. Le modèle est linéaire :
lmin = 1247 /U avec U en kV et lmin en pm.
Donner l’expression littérale du coefficient directeur a de la droite obtenue en fonction de h, c et e.
a = hc / e.
En déduire une valeur expérimentale de la constante de Planck h. Commenter.
h = a e / c avec a = 1247 10-12 x 103 =1,247 10-6 m V.
h = 1,247 10-6 *1,60 10-19 / (3,00 108)=6,65 10-34 J s.
Ecart relatif :(6,65-6,63) / 6,63 = 0,003 ( 0,3 %).
|
.
|
|
Détermination du matériau de l’anode du tube à rayons X utilisé
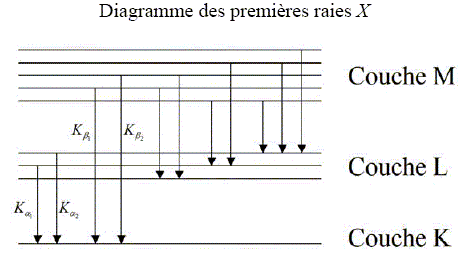
Illustrer le paragraphe « Les électrons peuvent également exciter
les atomes de la cible ; la lacune électronique provoquée est suivie
d’une réorganisation quasi-instantanée du cortège électronique qui se
traduit par l’émission de photons X de fluorescence » par un ou
plusieurs schémas légendés et expliquer les phénomènes physiques mis en
jeu.
En pénétrant dans l’anode, un
électron proche du noyau d’un atome peut être éjecté.
L’atome ne reste pas dans cet état instable
et excité. Le trou laissé est aussitôt
comblé par un électron d’une orbite plus
extérieure.
Lors de ce réarrangement, l’atome
émet un rayon X pour libérer son excès
d’énergie. L’énergie du rayonnement
X est caractéristique de chaque élément
chimique.
Calculer, en keV, l’énergie des deux raies de fluorescence notées Ka et Kß sur le spectre donné.
Ea = hc / la =6,63 10-34 *3,00 108 /(71,1 10-12)=2,79 10-15 J = 17,4 keV.
Eß =hc / lß=6,63 10-34 *3,00 108 /(63,1 10-12)=3,15 10-15 J = 19,7 keV.
En utilisant le tableau suivant, déterminer le matériau
constituant l’anode du tube à rayons X utilisé dans cette expérience.
Essai
|
Tungstène
|
Molybdène
|
Rhodium
|
Niveau K ( keV)
|
-69,5
|
-20,0
|
-23,2
|
Niveau L ( keV)
|
-11,3
|
-2,50
|
-3,14
|
Niveau M ( keV)
|
-2,3
|
-0,30
|
-0,41
|
Le métal est le molybdène. Ea =-2,5 +20 = 17,5 keV et Eß =-0,30 +20 = 19,7 keV.
Analyse par fluorescence X.
Le tube à rayons X précédent est utilisé comme source dite « primaire »
afin d’exciter l’échantillon à analyser. Celui-ci, en se désexcitant,
émet un rayonnement « secondaire » caractéristique qui est envoyé sur
un cristal analyseur couplé à un détecteur.
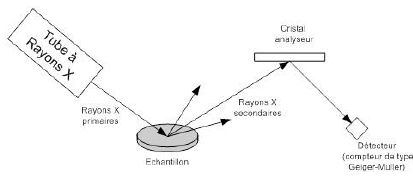
Le cristal analyseur est taillé de telle sorte que les atomes
constitutifs forment des plans parallèles à la surface, séparés entre
eux d’une distance d. Il se comporte comme un réseau de diffraction par
réflexion :
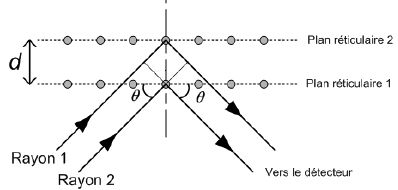
La condition (dite « loi de Bragg ») à laquelle doivent obéir les
rayons X secondaires 1 et 2 pour donner naissance à des interférences
constructives sur le détecteur s’écrit :
kl = 2d sin q.
avec k : nombre entier appelé « ordre de diffraction » ;
l : longueur d’onde des rayons X arrivant sur le cristal ;
q : angle de Bragg, angle entre le rayon incident et la surface du détecteur;
d : distance inter-réticulaire c'est-à-dire entre deux plans réticulaires.
En choisissant un cristal analyseur (c'est-à-dire en fixant la valeur
de d) et en choisissant l’angle de détection (c'est-à-dire en fixant la
valeur de l’angle q),
on peut donc isoler les radiations de longueurs d’onde qui satisfont à
la loi de Bragg. Dans le cas des appareils à canaux fixes, on installe
autour de l’échantillon plusieurs ensembles cristal-détecteur ; chaque
couple (d,q) fixé permet ainsi d’isoler une longueur d’onde et donc de repérer un élément prédéfini de l’échantillon.
Canal
|
Cristal analyseur
|
d(ppm)
|
q(°)
|
l(ppm)
|
A
|
Fluorure de lithium
|
201
|
28,9
|
2*201 sin 28,9 =194
|
B
|
Fluorure de lithium |
201
|
31,7
|
2*201 sin 31,7 =211 |
C
|
Fluorure de sodium
|
463
|
14,4
|
2*463 sin 14,4 =230 |
Pour chaque canal, déterminer la valeur de la longueur d’onde isolée si
l’on travaille au premier ordre, soit k = 1. Exprimer la en pm.
Lors de l’analyse d’une pastille de combustible de substitution,
le technicien détecte un signal uniquement sur les canaux A et C. Parmi
les éléments chimiques proposés ci-dessous, quels sont ceux
susceptibles d’être présents dans le combustible de substitution ?
Elément
|
Vanadium
|
Chrome
|
Manganèse
|
Fer
|
longueur d'onde caractéristique ( pm)
|
251
|
230
|
211
|
194
|
Le chrome et le fer sont présents.
|
|
Sécurité du technicien.
À proximité du tube à rayons X, le débit de dose peut atteindre 10 Sv.h-1. Pour la protection du technicien, ce débit est ramené à 1,0 µSv.h-1 (ordre de grandeur de la dose d’irradiation naturelle) par l’utilisation de vitres blindées en verre au plomb.
Déterminer le coefficient linéique d’atténuation µ du verre au plomb
utilisé sachant que sa CDA (couche de demi-atténuation) est de 0,35 mm.
µ CDA = ln 2 ; µ = ln2 / CDA =ln2 / 0,35 =1,98 ~2,0 mm-1.
Quelle est l’épaisseur minimale des vitres de blindage nécessaire à la protection du technicien ?
Loi de l'atténuation d'un faisceau monochromatique par un objet de densité uniforme : I = I0 exp(-µ x).
I0 :
flux de rayons X incident ; I :flux de rayons X sortant ; µ :
coefficient d'atténuation linéique du milieu ; L : épaisseur du milieu
traversé.
x = ln( I0 / I) / µ =ln(10 / 10-6) / 1,98 =8,1 mm.
|
|
|