Spectrophotométrie:
solution de lugol.
Bts biotechnologies 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
I.
Etude du spectrophotomètre.
Le
spectrophotomètre exploite une gamme de longueur d'onde allant de 350
nm à 750 nm. Son monochromateur comporte un réseau possédant1200 traits
par mm. La formule du réseau est :
sin q-sin
i = k n l.
1.1.
Donner la signification des différents termes et préciser les unités
dans le système internationnal.
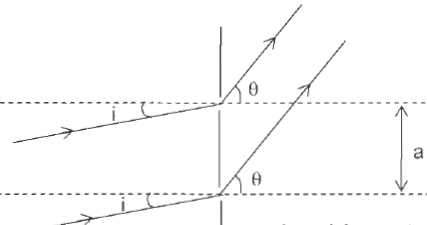
i : angle
d'incidence ( degré) ; q
: angle d'émergence ( degré) ;
l :
(mètre) longueur d'onde de la lumière monochromatique éclairant le
réseau ;
k : ordre de
difraction ; k est un entier, positif, négatif ou nul.
a
= 1/ n, pas du réseau (m) ; n : nombre de traits par unité de
longueur.
1.2.
Donner la définition du pas du réseau.
a = 1/n avec n = 1200 103 traits par mètre ; a =
8,33 10-7 m.
1.3.
Le réseau est utilisé en
incidence normale. Déterminer les angles d'émergence correspondant aux
deux extrémités du spectre pour l'ordre 1.
sin
q
= n l.
sin
q1
=1,2 106 *350 10-9 = 0,42
; q1 =
24,8°.
sin q2
=1,2 106 *750 10-9 = 0,90
; q2 =
64,2°.
2. Dosage
par spectrophotométrie.
Le
technicien a préparé deux solutions aqueuses de diiode dans l'iodure de
potassium pour différentes concentrations en diiode, et a
réalisé
la courbe d'étalonnage donnée ci-dessous.
La solution aqueuse de Lugol à tester est diluée 100 fois. Cette
solution est notée S1. L'absorbance de S1
vaut 1,4.
2.1.
Enoncer la loi de Beer-Lambert en précisant la signification de chaque
terme.
A= elc ( A est l'absorbance
ou densité optique).
où e est un coefficient
caractéristique de la substance appelé coefficient d'absorbance (L
mol-1 cm-1), l est l'épaisseur de la cuve (cm) et c la concentration de la solution
(mol/L).
2.2. Expliquer en
quoi la loi de Beer-Lambert est bien vérifiée ?
La courbe est une droite passant par l'origine.
2.3.
Déterminer la concentration molaire C1 de la
solution S1 puis la concentration molaire S0
de la solution S0.
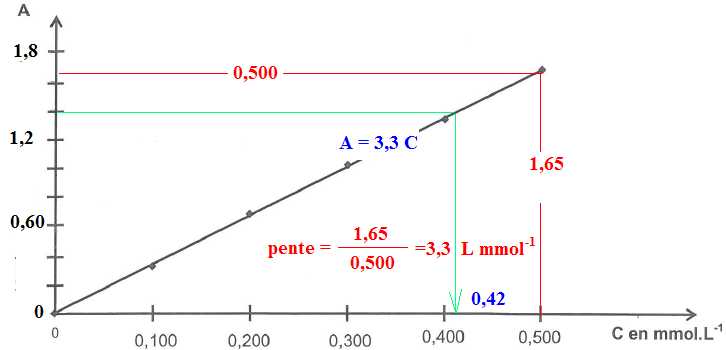
C1
= 0,42 mmol / L ; C0 =100 C1
= 42 mmol / L = 0,042 mol/L.
2.4.
La concentration massique en diiode de l'ancien flacon S0
est-elle compatible avec les caractéristiques attendues pour le test de
Cram (1,0 g de diiode et 2,0 g d'iodure de potassium pour 100 mL de
solution et la concentration en diiode ne doit pas s'écarte de plus de
10 % de la concentration préconisée) ?
Concentration massique en diiode de S0 : C0
M(I2) = 0,042 *2*127 ~10,7 g / l soit 1,07 g de
diiode dans 100 mL. L'ancien flacon de Lugol est donc compatible.
2.5. Pourquoi avoir
dilué 100 fois S0 ?
Sans dilution, l'absorbance serait égale à 140. Cette valeur sort de la
plage de mesure d'absorbance du spectrophotomètre.
|
| .
. |
|
|
Partie
2. Chimie générale.
1.
Dosage par titrage.
On dose un volume V1 =20,0 mL de la solution S1
avec une solution aqueuse de thiosulfate de sodium
(2Na+
+ S2032-) de concentration C2
= 2,0 10-3 mol.L-1. On
observe l’équivalence lorsqu’on a versé un volume VE
= 8,1 mL de solution titrante.
1.1.
Ecrire les demi-équations asociées aux deux couples oxydant / réducteur
mis en jeu.
2S2032-aq =S4062-aq +2e-.
I2 aq+2e- = 2I-aq.
1.2 Écrire
l’équation bilan de la réaction de titrage.
2 S2032-aq +I2 aq
---> S4062-aq +2I- aq .
1.3.
Calculer l'enthalpie standard DrG°
de cette réaction, ainsi que sa constante d'équilibre K à 298 K.
DrG°
=- E°(I2 aq / I- aq)-E°(S4062-aq / S2032-aq) * (2F)= -(0,62 -0,09)
*2*96500= -1,02 105 J mol-1.
DrG°
= -RT ln K ; ln K = 1,02 105
/ (8,314*298)=41,2. K = 8,5 1017.
1.4.
La valeur de cette constante est-elle compatible avec l'utilisation de
cette réaction pour réaliser ce titrage ?
Une réaction support d'un titrage doit être totale et rapide.
Une réaction totale possède une grande constante d'équilibre.
1.5.
Calculer C1 puis C0.
A l'équivalence n(S2032-aq) =2n(I2 aq).
C2VE = 2V0
C1 ; C1 =C2VE
/( 2V0 )=2,0 10-3 *8,1
/(2*20)=4,05 10-4 mol/L.
C0 = 100 C1 = 4,05 10-2
mol/L.
1.6.
Calculer la concentration massique Cm0 en diiode
de la solution S0. Conclure.
Cm0 = C0 M(I2)=4,05 10-2
*2*127=10,3 g/L.
Ce résultat est compatible avec celui obtenu par spectroscopie.
|
|
|
|
2.
Réflexion sur l'obtention d'une solution aqueuse de Lugol.
Le diiode est un solide violet qui se dissout faiblement dans l'eau
selon l'équation : I2(s) = I2aq
(1).
La solubilité du diiode dans l'eau pure est s = 1,34 10-3
mol/L.
2.1.
Calculer la concetration massique Cm d'une
solution aqueuse saturée de diiode.
Cm = s M(I2)=1,34 10-3
*2*127=0,34 g/L.
2.2. Une solution aqueuse de lugol est
obtenue en dissolvant 1,0 g de diiode et 2,0 g d'iodure de potassium
dans 100 mL d'eau. Montrer que le diiode se dissout plus facilement en
solution aqueuse contenant des ions iodure que dans l'eau pure.
On peut dissoudre 10 g de diiode solide par litre de solution contenant
20 g/L d'iodure de potassium. C'est 30 fois plus que dans l'eau pure.
2.3. En solution
aqueuse le diiode et les ions iodure donnent un complexe de formule I3-aq
selon l'équation :
I2aq +I-aq = I3-aq
(2).
La constante de formation de ce complexe est KF
=7,50 102.
-
Exprimer KF en fonction
des concentrations molaires.
KF = [I3-aq] / ([I-aq][I2aq]).
- Quel
est l'influence de l'ajout des ions iodures sur l'équilibre (2) ?
Un excès d'ion iodure déplace cet équilibre dans le sens direct.
- En
déduire l'influence de l'ajout des ions iodure sur la solubiilité du
diiode.
(1) +(2) donne : I2(s) +I-aq = I3-aq.
K = [I3-aq] / [I-aq] = s KF =1,34 10-3
*750 =1,0.
Solution de lugol : [I-aq] =20 / (127+40)~0,12 mol/L.
[I3-aq] =K [I-aq] ~0,12 mol/L soit 0,12*2*127 = 30,5
g/L.
En présence d'ion iodure, la solubilité du diiode augmente fortement.
|
|
|
|