Voiture à faible
consommation. Bts Ava 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
L'essence
peut être modélisée par l'octane C8H18 de masse
volumique r =750
g/L. Pouvoir thermique de l'essence 35000 kJ / L.
Equation de la combustion complète de l'essence :
C8H18 (l)+
12,5O2 (g)---> 8 CO2 (g)+ 9H2O (l).
Calculer la masse de dioxyde de carbone produite par la combustion
complète d'un litre d'essence.
Masse d'octane : m = 750
g ; M(octane) = 8*12+18 =114 g/mol.
Quantité de matière
d'octane n = m / M(octane) = 750 / 114 = 6,579 mol.
Quantité de matière de
dioxyde de carbone : 8 n = 52,63 mol.
Masse de dioxyde de
carbone : 8 n M(CO2) =52,63 *44 = 2,316 103
g ~2,3 kg.
la voiture consomme 3,8 L d'essence aux 100 km. Retrouver la masse de CO2
émis par km.
3,8 *2,316 / 100 = 88 g / km.
Pourquoi cherche-t-on à minimiser l'émission de CO2 par les
voitures ?
Afin de diminuer l'effet
de serre, le CO2 en étant l'un des principaux responsable.
La voiture roule à 90 km/h avec une consommation réelle de 4,8 L / 100
km. la force motrice permettant de maintenir cette vitesse a une valeur
constante F = 320 N.
Calculer la puissance mécanique de la voiture.
P = F v avec v = 90 / 3,6
=25 m/s ; P = 320*25 = 8,0 kW.
Déterminer l'énergie thermique fournie en une heure par l'essence au
moteur.
35 000 *4,8 =1,68 105 ~1,7 105 kJ.
Calculer le rendement du moteur.
Puissance thermique =1,68 105 /3600 =46,66 kW.
Rendement : 8,0 / 46,66 = 0,171 ( 17 %).
Sachant que le rendement de ce moteur à
essence est de 30 %, comment expliquer la différence de valeur avec le
résultat précédent ?
L'essence n'est pas constituée
que d'octane et sa combustion n'est pas complète. La puiisance mécanique sur l'arbre moteur
n'est pas complètement convertie en puissance propulsive.
|
| .
. |
|
|
Un camion de masse totale m = 40 t roule
sur autoroute. A l'approche d'une descente rectiligne de 500 m de long
à 4 %, le chauffeur règle le régulateur de vitesse sur 85 km/h et
active les systèmes automatiques de freinage sur l'échappement et de
frein moteur par compression.
Puissance du frein sur échappement : 185 kW à 2300 tr/min ; puissance
du frein moteur par compression : 375 kW à 2300 tr/min.
Dénivellation correspondant à une pente rectilligne de longueur 500 m à
4 % : 20 m.
Force de résistance de l'air à 85 km/h : Fair = 3000 N ;
force de résistance au roulement : Frr = 4300 N.
Schémtisser, sans souci d'échelle, la situation.
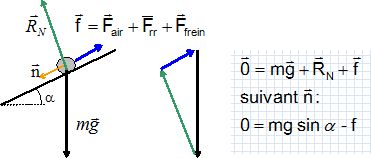
Pourquoi le travail de la réaction normale de la route est-il nulle ?
La réaction normale de la route étant perpendiculaire à la vitesse ne
travaille pas.
Calculer le travail de l'ensemble des forces de
frottements.
Travail résistant des
forces de frottement :
WF air +F rr = -(Fair +Frr) AB =
-(3000 +4300) *500 = -3,65 106 J.
Calculer le travail du poids au cours de la descente.
Travail moteur du poids
en descente : WP = mg h = 40 103*9,81
*20 =7,85 106 J.
En roues libres, comment évolue la vitesse du camion
en descente ?
Théorème de l'énergie cinétique au cours de la descente :
½m(v2finale- v2initiale )= WF air +F rr +WP
positif.
La vitesse croît.
Calculer le travail du système de freinage afin que
la vitesse reste constante.
La somme des travaux des
forces doit être nulle : WF air +F rr +WP
positif + Wf=0.
Wf
= -(7,85 +3,65) 106 = - 4,2
106 J.
La descente avec régulateur de vitesse s'effectue en
21 s ; en déduire la puissance moyenne des systèmes de freinage. Déterminer si le chauffeur doit
appuyer ou non sur la pédale de frein.
4,2 106 / 21 =2,0 105 W
( ~ 200 kW ).
Cette valeur étant inférieure à la puissance du système automatique de
freinage, le chauffeur ne freine pas.
|
.
|
|
Température du liquide de
refroidissement.
La plupart des capteurs de température utilisent un élément dont la
résistance varie avec la température. On donne les caractéristiques de
ce capteur :
R-10 °C =16674 ohms ; R 20 °C =3750 ohms ; R100°C
= 205 ohms.
Le pont diviseur de tension suivant permet d'obtenir une tension Us
qui varie en fonction de la résistance du capteur de température.
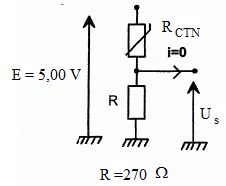
Exprimer Us en fonction de E, R et RCTN .
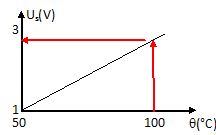
Calculer sa valeur si la CTN se trouve dans le liquide de
refroidissement à 100 °C. Le vérifier graphiquement.
E =(RCTN
+R) i ; Us =R i soit i = Us/R
; E = (RCTN / R +
1) Us ; Us = E / (RCTN / R + 1).
Us =5,00 / (205 / 270 +1) =2,84 V.
A l'atelier, à température ambiante, comment pourrait-on vérifier avec
un multimètre le bon état du capteur de température ?
A 20°C, le multimètre en
position ohmmètre ( circuit non parcouru par un courant), branché sur
le capteur doit indiquer environ 3750 ohms.
Ce capteur est associé à un conditionneut intégré au calculateur du
véhicule pour mesurer la température q du liquide de
refroidissement entre 50°C et 110°C. Une tension analogique Ua
variant linéairement de 0 à 5,00 V en fonction de la température est
fournie en sortie du conditionneur à partir de la tension Us
mesurée aux bornes du capteur.
Ua = 0 pour q =
50°C et Ua = 5,00 V pour q = 110°C.
La tension Ua est entachée d'une erreur maximale de ±50 mV
ce qui correspond à une erreur sur la température de ±0,6°C.
Cette tension Ua est nuérisée par un CAN. Deux CAN 12 bits
sont proposés :
ADS 1015 Q1 : 3,3 103 conversions par seconde ; erreur
maximale en V : ±(1 LSB +0,5 % UPE).
ADS 1000 Q1 : 128
conversions par seconde ; erreur maximale en V : ±(3 LSB +0,1 % UPE).
Pour faire un choix, il faut prendre en compte trois critères : la
résolution, la précision et la rapidité de conversion du CAN.
Montrer que le quantum de résolution de ces deux CAN vaut 1,22 mV.
q = 5,00 / 212
=1,22 10-3 V = 1,22 mV.
Comparer cette résolution à l'erreur maximale sur la tension Ua
et conclure.
e = xq +0,01 UPE
= 1*1,22 10-3+0,5 *5,00 / 100 =26,2 10-3 V = 26,2
mV pour le premier CAN et e = xq +0,01 UPE
= 3*1,22 10-3+0,1 *5,00 / 100 =8,75 10-3
V = 8,75 mV pour le second CAN. Le CAN ADS 1000
Q1 est le plus précis. De
plus 8,75 mV est bien inférieur à l'erreur maximale sur la
tension Ua.
Pour le CAN ADS 1000 Q1,
calculer l'intervalle de temps qui sépare deux conversions successives.
1/128 =7,81 10-3
s = 7,81 ms.
La fréquence de conversion de ce CAN est-elle suffisante pour
communiquer à l'ordinateur de bord la température du moteur ?
Durée d'un cycle moteur à
2300 tr/min : 60 / 2300 = 2,6 10-2 s = 26 ms. L'inertie thermique du moteur
est grande. La fréquence de conversion du CAN CAN ADS 1000
Q1 est donc suffisante.
|
|