Fibroscopie.
Bts analyes de biologie médicale 2015.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
|
Les cellules cancéreuses se distinguent des cellules saines de plusieurs manières : en
particulier, la fluorescence des cellules malades n’est pas la même que celle des cellules normales.
La technique décrite ici se base sur la capacité qu’ont les molécules
de tryptophane et de NADH (forme réduite de la nicotinamide adénine
dinucléotide) d’émettre une fluorescence respectivement à 360 nm et à
440 nm lorsqu’elles sont excitées par une radiation de longueur d’onde
308 nm.
Le dessin ci-dessous décrit le principe d’observation : le
fibroscope utilisé est constitué d’un ensemble de fibres optiques, les
fibres excitatrices et les fibres réceptrices.
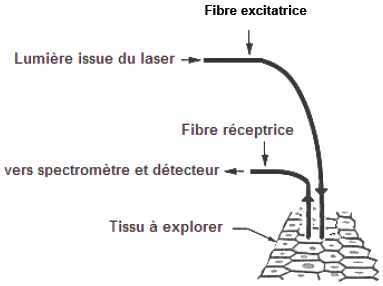
Les fibres excitatrices éclairent le tissu avec la radiation d’excitation produite par un laser.
Les
fibres réceptrices guident la lumière émise par le tissu vers un
spectrophotomètre puis un détecteur permettant d’enregistrer le spectre
correspondant. Le spectre obtenu permet de déterminer le rapport R=I360 / I440
entre les intensités de fluorescence obtenues à 360 nm et à 440 nm. On
estime que si ce rapport est inférieur à 1 le tissu est sain alors que
s’il dépasse largement 2, le tissu est tumoral.
Partie 1: éclairement des tissus via la fibre optique excitatrice.
1.1 Le rayonnement laser est qualifié de lumière monochromatique. Définir ce terme.
Une lumière monochromatique possède une seule couleur ( une seule fréquence ).
1.2
La longueur d’onde de 308 nm choisie pour éclairer le tissu via la
fibre optique excitatrice est-elle cohérente par rapport à l’extrait de
brochure sur le laser ci-dessus ?
"illuminer avec de la lumière UV des cellules de la vessie".
308 nm est inférieure à 400 nm : cette longueur d'onde appartient au domaine UV.
On
s’intéresse ici au cas de la fibre à saut d’indice. Une telle fibre
optique est constituée d’un coeur en verre d’indice optique nc entouré d’une gaine d’indice optique ng.
La propagation de la lumière dans la fibre peut se modéliser par les
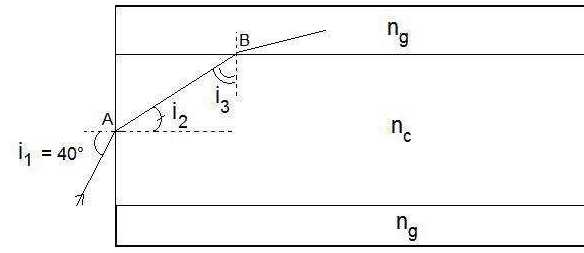
lois de la réfraction. Le schéma ci-dessous modélise le trajet d’un
rayon lumineux dans la fibre. Le coeur possède un indice nc qui vaut 1,62 et la gaine possède un indice ng qui vaut 1,51. On considère que l’indice optique de l’air vaut 1,00.
On s’intéresse à ce qui se passe au niveau des points A et B dans le cas où l’angle d’incidence i1 vaut 40°.
1.3 Rappeler les lois de Snell-Descartes relatives à la réfraction.
Rayons incident et réfracté sont dans le même plan.
n1 sin i1 = n2 sin i2.
1.4 Calculer la valeur de l’angle i2.
sin i2 = n1 sin i1 / nc =1 sin 40 / 1,62 =0,397 ; i2 = 23,38 ~23°. 1.5 Montrer que l’angle i3 a pour valeur environ 67°.
Les angles i2 et i3 sont complémentaires.
i2 +i3 = 90° ; i3 = 90-23,38 =66,62 ~67°.
Pour que le rayon qui arrive en B reste dans le coeur de la fibre, il faut qu’il y subisse une réflexion totale.
1.6 Expliquer pourquoi en arrivant sur le point B, le rayon lumineux arrivant avec l’incidence i3 précédente peut passer dans la gaine.
Au point B : nc sin i3 = ng sin i4.
sin i4 = nc sin i3 / ng =1,62 sin 66,62 / 1,51 = 0,985 ;
Cette valeur étant inférieure à 1, le rayon réfracté dans la gaine existe bien.
|
| .
. |
|
|
L’angle d’incidence limite iL
en B, c'est-à-dire l’angle au-delà duquel la réflexion est totale, est
alors calculé en considérant que le sinus de l’angle réfracté dans la
gaine vaut 1,0.
1.7 Montrer que dans le cas de la fibre étudiée la valeur de l’angle d’incidence limite iL est située entre 68 et 69°.
Au point B : nc sin iL = ng sin 90.
sin iL = ng / nc =1,51 / 1,62 = 0,932 ; iL = 68,76°.
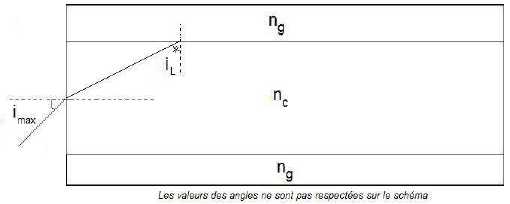
On
définit l’ouverture numérique (ON) de la fibre comme le sinus de
l’angle d’incidence dans la fibre qui engendre, dans le coeur de la
fibre, un angle réfracté correspondant à l’angle limite au point B.
L’angle imax définit alors le demi-angle au sommet du cône d’acceptance de la fibre. On montre mathématiquement que ON = sin imax = ( nc2-ng2 )½.
1.8 Déterminer le demi-angle au sommet imax du cône d’acceptance de la fibre étudiée.
sin imax = ( 1,622-1,512 )½= 0,587 ; imax = 35,93 ~36°.
1.9 Ce résultat est-il cohérent avec la situation décrite dans les questions 1.4 à 1.6 ?
Oui, l'angle i1 valant 40° supérieur à imax, n'appartient pas au cône d'acceptance de la fibre.
|
|
|
|
Partie 2 : exploitation du phénomène de fluorescence.
On
modélise de façon simple le mécanisme énergétique mis en jeu lors du
phénomène de fluorescence moléculaire du tryptophane de la façon
suivante : sans sollicitation extérieure la molécule de tryptophane est
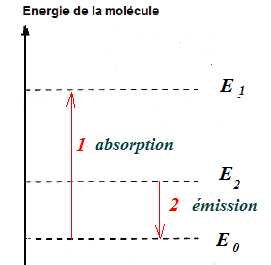
dans son état « fondamental » stable E0. Lorsqu’elle est soumise à un rayonnement de longueur d’onde l1 = 308 nm, elle est excitée et portée dans un état d’énergie E1. Elle se désexcite sans émettre de radiation vers un état d’énergie E2, différent de E0, puis retourne depuis l’état d’énergie E2 à l’état fondamental en émettant un rayonnement de longueur d’onde λ2 = 360 nm.
2.1 Placer sur le diagramme , au niveau des pointillés, les états d’énergie E0, E1 et E2.
2.2 Représenter, sur ce diagramme, par des flèches repérées par 1 et 2 les transitions permettant :
- d’exciter la molécule vers l’état E1 depuis l’état fondamental (flèche 1).
- de retourner à l’état fondamental depuis l’état d’énergie E2 (flèche 2).
2.3
Préciser, sur ce diagramme, pour chacune des transitions précédentes
s’il s’agit d’une absorption ou d’une émission de rayonnement.
L’exploration d’un tissu par la méthode décrite plus haut conduit à l’enregistrement du spectre suivant.
2.4 Le tissu exploré est-il sain ? Justifier clairement la réponse.
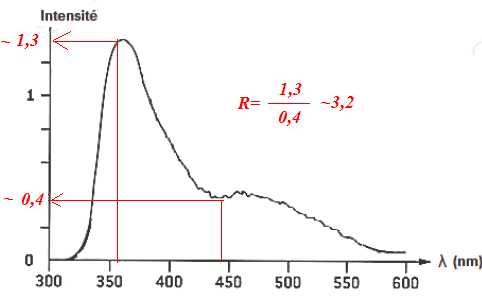
R étant supérieur à 2, le tissu est tumoral.
|
|
|
|