Suivi du niveau de
la mer par le satellite Saral. Bac S Amérique du sud 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
|
Le
niveau moyen des océans est un des indicateurs les plus importants du
réchauffement climatique. Son suivi, grâce notamment aux satellites
altimétriques, est d'une importance
majeure pour la compréhension de l’évolution du climat. Actuellement une configuration de cinq
satellites altimétriques est disponible : Jason-1, Envisat, Jason-2, Cryosat-2 et Saral. Elle permet
d'obtenir un grand nombre de données.
La plus récente mission altimétrique, celle du satellite Saral, lancé le 25 février 2013, est le fruit
d'une collaboration entre la France et l’Inde.
Données :
- célérité des ondes électromagnétiques dans l’ionosphère : c = 2,99 792 × 108 m.s-1 ;
- rayon moyen de la Terre : R = 6371 km ;
- période de rotation de la Terre : TT = 23,93 heures ;
- masse de la Terre : M = 5,98 × 1024 kg ;
- masse de Saral : MS = 400 kg ;
- constante de gravitation universelle : G = 6,67 × 10-11 m3.kg–1.s–2 ;
- altitude moyenne du satellite h = 800 km ;
- vitesse orbitale du satellite 7,47 km/s.
- période du satellite : 100,59 min.
Étude des caractéristiques du mouvement de Saral.
Le mouvement du satellite Saral est étudié dans le référentiel géocentrique supposé galiléen.
On suppose dans cette partie que l’orbite du satellite Saral est circulaire.
1.1. Énoncer la
seconde loi de Kepler appliquée au satellite étudié. Quelle précision
nous apporte-elle sur le mouvement du satellite ?
Deuxième loi ou loi des
aires : le mouvement de chaque planète est
tel que le segment de droite reliant le soleil et la
planète balaie des aires
égales pendant des durées
égales.
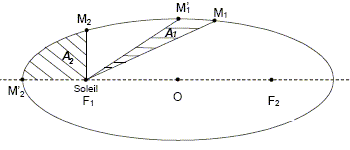Les aires A1 et A2 sont égales.
Schématiser la trajectoire du satellite et représenter, en un point de cette trajectoire, son vecteur
vitesse et son vecteur accélération sans souci d’échelle.
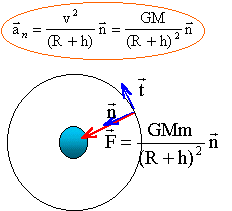
Le satellite est soumis
à la seule force de gravitation centripète
exercée par la planète.
|
| .
. |
|
|
1.2. Montrer que l’expression de la vitesse du satellite Saral est v=(G.M/(R+h))½,
puis calculer sa valeur.Comparer avec les informations données sur ce
satellite. L’hypothèse d’une trajectoire circulaire est-elle cohérente ?
Suivant l'axe n la
seconde loi de Newton s'écrit : GMm /(R+h)2 = m
aN= mv2/ (R+h)
d'où la valeur de la vitesse (m/s):
v =(GM / (R+h))½.
v = (6,67 10-11 * 5,98 1024 / (6,371 106 +8,00 105))½ =7458 m/s ~7,46 km/s.
Cette valeur est en accord avec la vitesse donnée. L'hypothèse d'une trajectoire circulaire est correcte.
1.3. Établir l’expression de la période de révolution TS du satellite Saral autour de la Terre. Calculer sa valeur et la comparer avec les informations données sur ce satellite.
Le satellite décrit la circonférence 2p(R+h) à la vitesse v en TS seconde.
2p(R+h) = v TS ; TS =2p(R+h) / v.
TS =2*3,14(6,371 106 +8,00 105) / 7458=6,04 103 s ou ~100 min, en accord avec les données.
|
|
|
|
Évaluation du niveau de la mer Méditerranée grâce aux satellites altimétriques.
La mer Méditerranée a une superficie de 2 515 000 km2, sa profondeur moyenne est de 1 500 m et l'abysse la plus profonde est de 5 121 m.
Le 1er août 2013, le satellite altimétrique Saral, dont
l’altitude par rapport à la surface de référence est 813 474 m, mesure
un décalage temporel Dt de 5,40296 ms entre l’émission et la réception de l’onde dans l’ionosphère.
2.1. Pourquoi les radars altimètres utilisent-ils les micro-ondes ?
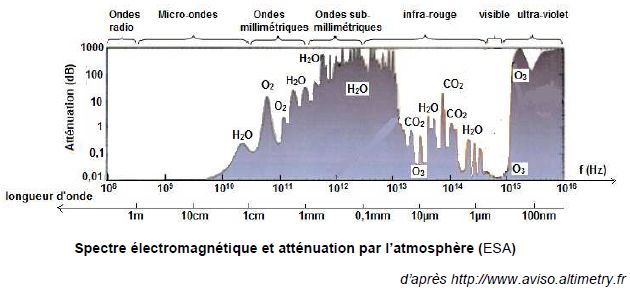
Les micro-ondes sont très peu atténuées par l'atmosphère.
2.2. Pourquoi Saral n’utilise-t-il qu’une seule bande de fréquence contrairement aux autres satellites altimétriques ?
La bande de fréquence utilisée par Saral est très peu sensible aux perturbations ionosphériques.
2.3. Déterminer la
valeur de la hauteur SSH qui repère le niveau de la mer Méditerranée à
l’endroit de la mesure prise par le satellite Saral le 1er août 2013.
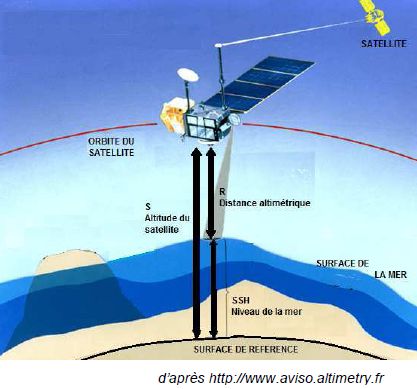
Un radar altimètre embarqué à bord d'un satellite émet un signal à très
haute fréquence à la verticale de celui-ci en direction du sol et
reçoit en retour l'écho réfléchi par la surface de la mer.
R =½c Dt = 0,5 *2,99 792 108 *5,40296 10-3 = 8,09882 105 m.
SSH = S-R = 813 474-809 882 =3,59191 km.
|
|
|
|