Dosage de la niacine, taurine et acide aminés, pendant la chute. Bac St2S Métropole 2015 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Dosage de la niacine dans une boisson énergétique. On souhaite vérifier une des indications de l’étiquette et, en particulier, mesurer la concentration molaire cn de niacine dans la boisson. Pour cela, on procède à un dosage acido-basique de la niacine contenue dans une canette de volume V égal à 250 mL. On verse le contenu de cette canette dans un bécher et on y ajoute progressivement une solution aqueuse d’hydroxyde de sodium (soude) de concentration molaire Cb égale à 1,5 x 10-2 mol L-1.  Indiquer parmi les deux solutions utilisées (boisson et solution aqueuse d’hydroxyde de sodium) laquelle est la solution à titrer. Justifier la réponse. La concentration de la solution à titrer contenue dans la canette est inconnue. La concentration de la solution titrante, la soude, est connue. On utilise pour réaliser ce dosage le montage représenté ci-dessous. Indiquer le nom des matériels repérés par les lettres B et D ainsi que des solutions repérées par les lettres A et C. 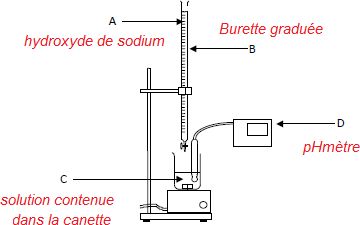Au cours du dosage, on relève régulièrement la valeur du pH du mélange réactionnel. On obtient le graphique pH = f(Vb) donné. On note AH la niacine, A– sa base conjuguée. L’équation bilan de la réaction du dosage s’écrit AH + HO–---> A– + H2O. Définir l’équivalence d’un dosage. A l'équivalence le quantités de matière des réactifs sont en proportions stoechiométriques. Avant l'équivalence, la niacine est en excès , après l'équivalence, la soude est en excès. Déterminer le volume Vb E de solution de soude versé à l’équivalence. Faire apparaître clairement la construction graphique réalisée. En déduire l’expression littérale de cn en fonction de V, cb et VbE. Montrer que la valeur de cn est égale à 6,5 x 10-4 mol L-1. 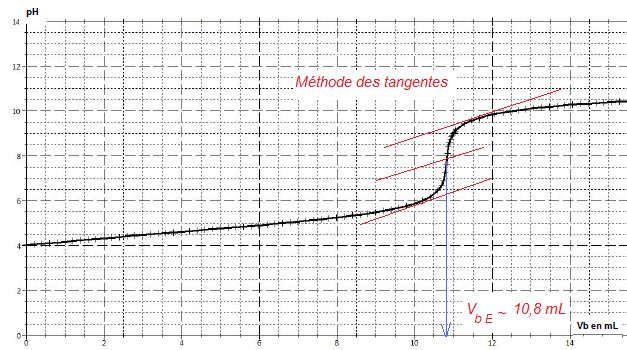A l’équivalence : quantité de matière de niacine : cn V ; quantité de matière de soude : cb Vb E. cn V = cb Vb E ; cn  = cb Vb E / V =1,5 10-2 *10,8 / 250 ~6,5 10-4 mol/L. La masse de niacine mn contenue dans une canette de volume V vérifie la relation mn = cn x Mn x V dans laquelle le volume V est exprimé en L. Calculer la masse de niacine contenue dans les 250 mL de boisson dosée. Donnée : M(niacine) = 123,1 g mol-1.  Comparer ce résultat avec celui de l’étiquette ( 8 mg pour 100 mL ). mn = cn x Mn x V =6,5 10-4 *123,1 *0,250 = 2,0 10-2 g = 20 mg. Soit 20 *100 / 250 =8 mg dans 100 mL, en accord avec l'étiquette.  Taurine et acide a aminé. La taurine n’est pas un acide a-aminé ; c’est un dérivé d’acide aminé. Il est synthétisé à partir de la cystéine. On le rencontre naturellement dans la viande et les produits laitiers. Recopier la formule de la cystéine et indiquer par un astérisque le(s) carbone(s) asymétrique(s) présent(s). Préciser si cette molécule est chirale. Justifier la réponse. Donner la représentation de Fischer d’une des deux configurations de la cystéine en précisant s’il s’agit de la configuration L ou de la configuration D. Une molécule possèdant un atome de carbone asymétrique est chirale. 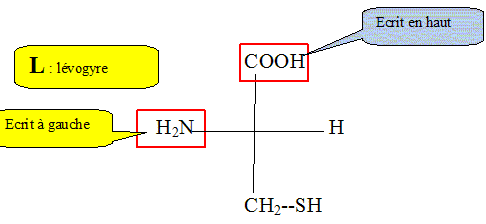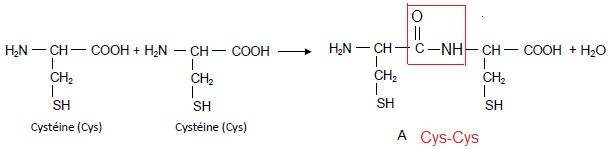La cystéine peut réagir pour former un dipeptide selon la réaction dont l’équation bilan est la suivante. Donner la formule semi-développée du composé A. Nommer le dipeptide obtenu en utilisant les abréviations. Entourer sur la formule du dipeptide la liaison peptidique. Une canette de boisson énergisante contient une quantité de taurine nt égale à 8,00 x 10-3 mol. Déterminer la formule brute de la taurine.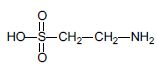 Montrer que la masse molaire de la taurine Mt vaut 125,1 g mol-1. En déduire la masse de taurine mt contenue dans une canette. Expliciter pourquoi on peut affirmer que cet apport est important. Taurine : C2H7O3NS ; Mt =2*12 +7+3*16+14+32,1 =125,1 g mol-1. mt = Mt mt =125,1*8,00 10-3 =1,00 g. La dose journalière de taurine apportée par l’alimentation dépasse rarement 200 mg par jour. La masse de taurine apportée par la boisson énergisante est donc importante. Pendant la chute. Partie A : Des conditions extrêmes. Lors de cette aventure, F. Baumgartner est équipé d’un scaphandre lui permettant de résister à des conditions très particulières. Le scaphandre est pressurisé. La pression de l’air dans le scaphandre patm est égale à 101,3 x 103 SI, valeur de la pression atmosphérique au sol le jour du saut. La visière du casque de F. Baumgartner a une surface d’aire S égale à 500 cm². On note F la valeur de la force pressante exercée par l’air placé dans le scaphandre sur la visière. On rappelle la relation p = F / S qui relie la pression p à la force pressante F exercée sur une surface S. Rappeler l’unité SI de pression. Pascal ( Pa). Montrer que la valeur de la force pressante F exercée par l’air contenu dans le scaphandre sur la visière a pour valeur 5 065 N. F =p S = 101,3 103 *500 10-4 =5065 N. A l’altitude de 38 970 m, l’atmosphère est extrêmement raréfiée et la pression extérieure peut être considérée comme nulle. Prévoir si la visière est éjectée ou plaquée contre le visage de F. Baumgartner, dans l’hypothèse où elle est mal fixée. Justifier la réponse. La force pressante exercée par l'air intérieur du scaphandre est dirigée vers l'extérieur. La visière peut être éjectée. Le scaphandre doit également protéger Baumgartner du rayonnement solaire, en particulier du rayonnement ultra-violet. Citer deux effets nocifs du rayonnement ultra-violet sur le corps humain. Les UV provoquent  des lésions dégénératives dans les cellules cutanées et une réaction inflammatoire de l'oeil. Partie B : Franchir le mur du son. Félix Baumgartner chute sans vitesse initiale depuis un point noté A, situé à 38 970 m d’altitude. Sa masse m, scaphandre et parachute compris, est égale à 120 kg. On considère que la seule force qu’il subit est son poids P force verticale dirigée vers le bas. On veut connaître la vitesse atteinte au point B situé à la verticale du point A, à une distance h égale à 6 955 m. On rappelle que P = m  g (on considère que g reste constant au cours de la chute.) Montrer que le poids P de Félix Baumgartner (équipement compris) vaut 1,2 x 103 N. Donnée : valeur approchée de l’intensité de pesanteur g = 10 N kg-1. P = mg = 120 *10 = 1,20 103 N.  Choisir parmi les propositions ci-dessous l’expression du travail du poids pendant cette chute. a) m g / h  ; b) m g h ;  c) – m g h. Le travail du poids est moteur en descente et vaut m g AB = m g h. Vérifier que le travail du poids durant cette chute vaut 8,3 x 106 J. WAB(P) =m g h = 120*10 *6955 =8,3 06 J. En appliquant le théorème de l’énergie cinétique à Félix Baumgartner lors de son passage du point A au point B, on a obtenu la relation suivante décrivant l’énergie cinétique du parachutiste en B, EC(B)  = WAB(P) Rappeler la relation entre l’énergie cinétique EC(B) au point B et la vitesse atteinte au point B, VB. EC(B) = ½mV2B. Calculer alors la vitesse VB en m s-1 puis en km h-1. Préciser si la valeur trouvée est en accord avec celle donnée dans le texte d’introduction ( 1342,8 km/ h ). ½mV2B = m g h ; V2B =2 g h ; VB = (2 g h)½ =(2*10*6955)½ =373 m /s ou 373*3,6 =1,34 103 km/h, en accord avec le texte. .

menu