Facteurs
accidentogènes, eau oxygénée, boissons non alcoolisées. Bac ST2S
Antilles 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
Définir
l’expression « Facteurs accidentogènes ». Donner
deux autres facteurs accidentogènes lors de la conduite d’un véhicule.
Les principaux facteurs d'accidents sur la
route sont, l'alcool au volant, l'excès de vitesse, le théléphone au
volant, la somnolence, la
drogue.
Citer
le facteur accidentogène évoqué dans les documents.
L'alcool au volant.
Une personne a bu de l’alcool au cours d’un repas, son alcoolémie est
celle du document suivant.
Indiquer à partir de quelle durée on peut considérer que son alcoolémie
est nulle.
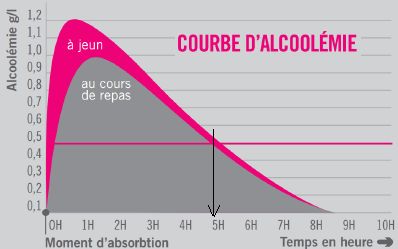
L'alcoolémie est nulle au
bout de 8 h 30 min.
Donner la durée pendant laquelle le risque que cette personne ait
un accident mortel est supérieur à deux fois celui d’un individu non
alcoolisé. Justifier la réponse.
A 0,5 g/L le risque
d'être impliqué dans un accident mortel est multiplié par 2. Pendant 5
heures ce risque persiste.
On se place dans le cas d’un véhicule de masse 800
kg roulant à une vitesse de 90 km h-1.
On considère que le temps de réaction d’un conducteur est égal à une
seconde.
Montrer que 90 km h-1 est équivalent à 25 m s-1.
90 / 3,6 =25 m s-1.
Calculer la distance parcourue par le véhicule pendant le temps de
réaction.
25 m sont parcourus en
une seconde.
Préciser si la valeur trouvée est-elle en accord avec la valeur
indiquée sur la plaquette de l’association. Justifier la réponse.
En accord avec le
document suivant :

Le véhicule se déplace sur une route horizontale. Le véhicule est
soumis à trois forces :
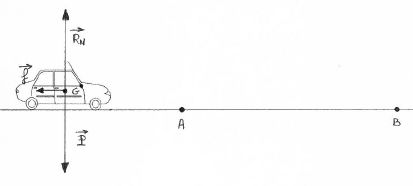
la force de freinage supposée constante et de valeur
f = 5600 N, le poids P ,
la force verticale exercée par la route, appelée réaction de la route RN.
Au point A, la vitesse du véhicule est de 90 km h-1. Au
point B, il s’est immobilisé.
|
|
|
Donner l’expression du travail de la force
de freinage WAB sur le trajet AB.
WAB
= - f AB
Justifier que le
travail des deux autres forces est nul.
Une force perpendiculaire
au déplacement ne travaille pas.
Montrer que
l’énergie cinétique du véhicule au point A est égale à : Ec
(A) = 2,5.105 J.
½mv2
= 0,5 *800*252 =2,5.105 J.
Justifier que l’énergie
cinétique du véhicule au point B, Ec (B), est nulle.
En B le véhicule est
immobile.
Le théorème de
l’énergie cinétique appliqué à la situation étudiée, conduit à
l’expression :
Ec (B) – Ec
(A) = WAB.
Calculer la distance de
freinage.
0-Ec (A) = -f AB ;
AB = Ec (A)/ f = 2,5 105
/ 5600 =44,6 ~45 m.
En accord avec la plaquette de
l’association.
On considère
l’affirmation du document 2 : « Circuler en ville la nuit à 90 km h-1
au lieu de 50 km h-1, ce n’est pas dangereux ». Prendre position à propos de cette
affirmation et justifier le point de vue adopté.
Cette affirmation est fausse, la distance
d'arrêt est de 70 m à 90 km/h au lieu de 26 m à 50 km / h.
|
|
|
L'eau oxygénée .
Donner la définition d’un oxydant.
Un oxydant est une espèce
suceptible de gagner un ou plusieurs électrons.
Associer aux numéros le nom de l’objet ou de la solution qui lui
correspond.
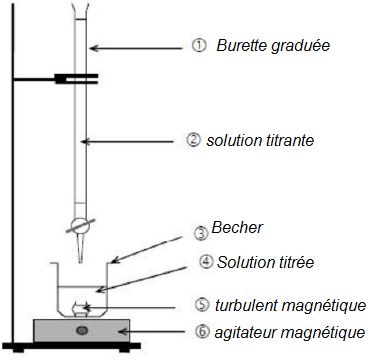
Nommer le matériel nécessaire utilisé pour prélever un volume d’eau
oxygénée de 20 mL.
Une pipette jaugée mesure
un volume précis.
L’équation de la réaction du dosage étudié est :
2MnO4- + 6H+ + 5H2O2
--->2Mn2+ +5O2 + 8H2O.
Les deux couples redox mis en jeu lors de ce dosage sont : MnO4-
/Mn2+ et O2 /H2O2
Lors de ce
dosage, nommer le réactif oxydant et le réactif réducteur.
MnO4- est
l'oxydant et H2O2 est le réducteur.
Définir l’équivalence d’un dosage.
A l'équivalence les
réactifs sont en proportions stoechiométriques. Avant
l'équivalence, H2O2 est en excès, après
l'équivalence MnO4- est en excès.
Préciser quelle observation permet de repérer l’équivalence lors du
dosage réalisé.
MnO4- est
la seule espèce colorée. A l'équivalence la solution passe de
l'incolore au violet.
On se place à l’équivalence du
dosage.
Donner la relation entre les quantités de matière n1 d’eau
oxygénée et n2 d’ions permanganate.
2 n1
= 5 n2.
En déduire la relation donnant la concentration de l’eau oxygénée dosée
C1 = 2,5 C2Véq / V1.
On prélève un volume V1
= 20,0 mL d’eau oxygénée : n1 = V1 C1 ; [MnO4-] = C2 = 0,60 mol/L ; Véq
= 10,1 mL ; n2 = C2Véq =0,60 *10,1 =
6,06 mmol
2V1 C1= 5 C2Véq ; C1 = 2,5 C2Véq
/ V1.
Calculer C1,
concentration de la solution d’eau oxygénée.
C1 = 2,5 *0 ,60 *10,1 / 20 =0,7575 ~ 0,76 mol/L.
Calculer le titre t de l’eau
oxygénée dosée. Expliquer en quoi l’analyse permet de déterminer
si cette solution est adaptée pour être utilisée comme désinfectant.
t = 11,2 C1
= 11,2 *0,7575 = 8,5 volumes.
Cette valeur étant
inférieure à 10 volumes, cette solution est adaptée.
|
Boissons non
alcoolisées.
Les
esters sont des dérivés des acides carboxyliques, ils résultent très
généralement de l'action d'un alcool sur ces acides avec élimination
d'eau. Les fonctions esters se retrouvent dans de
nombreuses molécules biologiques, notamment les triglycérides. Les
esters ont souvent une odeur agréable et sont à l'origine des arômes
naturels.
Ils sont aussi utilisés comme arômes synthétiques pour fabriquer des
boissons qui peuvent se substituer à l’alcool.
Etude du butanoate d’éthyle, arôme artificiel de banane.
Entourer et nommer les groupements fonctionnels présents. Ecrire la
formule semi-développée du butanoate d’éthyle. Nommer la molécule A.
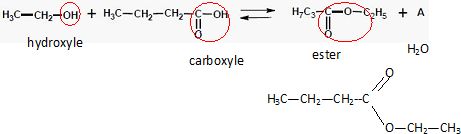
Donner deux caractéristiques de cette réaction.
Réaction lente et limitée
par l'hydrolyse de l'ester.
Choisir parmi les trois montages suivants celui correspondant à un
montage de chauffage à reflux.

Justifier
l’intérêt d’un montage de chauffage à reflux.
Le chauffage à reflux (
montage A) permet d'accélérer la réaction tout en évitant les pertes de
matière. Les vapeurs se condensent et retombent dans le milieu
réactionnel.
Parmi les propositions suivantes choisir celle qui
est exacte :
Proposition 1 : l’équation ci-dessus montre que pour un gramme d’alcool
qui a réagi, il se forme un gramme d’ester (butanoate d’éthyle).
Proposition 2 : l’équation ci-dessus montre que pour une mole d’alcool
qui a réagi, il se forme une mole d’ester (butanoate d’éthyle). Vrai.
Proposition 3 : l’équation ci-dessus montre que pour une mole d’alcool
qui a réagi, il se forme trois moles d’ester (butanoate d’éthyle).
On utilise m=0,92 g d’alcool (éthanol M = 46 g/mol).
Calculer le nombre de mole d’alcool introduit initialement.
m / M =0,92 / 46 = 0,020 mol.
En déduire le nombre de mole maximale de butanoate d’éthyle que
l’on pourrait obtenir si la réaction était totale. 0,020 mol.
Montrer que l’on pourrait alors obtenir
2,3 g d’ester lors de cette réaction.
M(ester) = 116 g/mol ;
0,020 *116 = 2,32 ~2,3 g.
La masse d’ester réellement formée au cours de cette réaction est de
1,54 g.
Calculer le rendement de cette réaction.
Masse réelle / masse
théorique = 1,54 / 2,32 ~0,66.
|
|
|