Le muon,
explorateur de volcan.
Bac S Polynésie 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
Les muons créés en haute atmosphère
Un muon créé à une hauteur de 20 km d'altitude doit mettre environ 67 μs pour arriver au sol.
1.1.1 Retrouver à
l’aide d’un calcul l’estimation faite de la valeur du temps de parcours
d’un muon créé à une altitude de 20 km pour arriver jusqu’au sol.
La vitesse des muons est proche de la vitesse de la lumière dans le vide.
Temps de parcours = 20 103 / (3,0 108) ~6,7 10-5 s = 67 µs.
Albert
Einstein publie en 1905 une nouvelle théorie intitulée « la relativité
restreinte » qui remet en cause la mécanique classique.
1.1.2 Énoncer le postulat d’Einstein relatif à la vitesse de la lumière.
La vitesse de la lumière dans le vide a la même valeur dans tous les référentiels galiléens.
1.1.3 Expliquer sans
calcul en quoi la détection d’un nombre important de muons au niveau de
la surface terrestre constitue une preuve expérimentale de la «
dilatation » des durées.
La durée de vie d'un muon
au repos ou durée mesurée dans le référentiel muon ( durée propre
) est de l'ordre de 2 µs. En 2 µs, un muon parcourt seulement environ 2
10-6 *3 108 ~ 6 102 m ~ 0,6 km. Or les muons sont produits à au moins 10 km de la surface de la terre et ils
parviennent en grand nombre, à la surface de la terre. Ils
parcourent donc une distance bien supérieure à 0,2 km. Vue de la terre,
leur durée de vie moyenne, lorsqu'il sont en mouvement, se dilate.
1.2 Pourquoi
peut-on dire que le muon, le proton et l’électron sont soumis à une
force magnétique de même intensité lorsqu’ils pénètrent à la même
vitesse dans un champ magnétique ?
Justifier
pourquoi la différence de courbure alors observée permet d’affirmer que
le muon a une masse intermédiaire entre celle du proton et celle de
l’électron.
Proton,
électron et muon possèdent, en valeur absolue, la même charge. La
valeur de la force magnétique appliquée à une particule chargée en
mouvement dans un champ magnétique est
proportionnelle à la vitessse, à la valeur absolue de la charge et au champ magnétique.
Le rayon de courbure de
la trajectoire d'une particule chargée en mouvement dans un champ
magnétique est proportionnel à la masse de la particule.
Pour une vitesse donnée, pour un champ magétique donnée et pour une
même charge ( en valeur absolue), le rayon de courbure de la
trajectoire est d'autant plus grand que la masse de la particule est
grande.
La trajectoire d'un muon étant plus incurvée ( rayon de courbure plus
faible ) que celle du proton, la masse du muon est inférieure à celle
d'un proton.
La
trajectoire d'un muon étant moins incurvée que celle de l'électron, la masse du muon est supérieure à celle
d'un électron.
Les muons au CERN.
2.1
Justifier à l’aide d’un calcul l’affirmation : « Ces muons ont un temps
de vie environ égal à 30 fois leur temps de vie au repos ».
Vitesse des muons v = 0,9994 c ; ß = v / c =0,9994 ; 1-ß2 ~1,2 10-3.
g = (1-ß2)-½ =(1,2 10-3)-½ ~ 29.
Le temps de vie d'un muon, mesuré dans le référentiel terrestre, est environ 29 fois sa durée de vie propre.
Bien qu’un muon ne puisse survivre plus de 14 ou 15 tours selon la
mécanique newtonienne, la plupart d’entre eux font plus de 400 tours.
2.2 Vérifier alors la cohérence entre les valeurs « 14 ou 15 tours » et « 400 tours » données.
On retrouve la valeur de g , rapport entre durée mesurée et durée propre : 400 / 14 ~29.
|
| .
. |
|
|
Les muons pour la tomographie d’un volcan.
La tomographie est une technique d’imagerie permettant de reconstruire le volume d’un objet à partir d’une série de mesures.
3.1 Expliquer pourquoi un muon ordinaire d’énergie moyenne de 4 GeV ne peut pas être utilisé pour radiographier la Soufrière.
Un muon perd en moyenne 2 MeV par centimètre de roche traversée.
Un muon d'énergie 4 GeV traverse donc : 4 103 / 2 = 2000 cm = 20 m de roche..
La radiographie muonique
nécessite des muons traversant plusieurs centaines de mètres de roches,
donc des muons d'énergie bien supérieure à 4 GeV.
Au niveau du sol, le flux moyen de muons est d’environ 1 muon par cm2 et par minute.
3.2.
Déterminer l’ordre de grandeur de l’énergie apportée pendant une minute
par le flux de muons ordinaires sur la surface de la Soufrière.
Comparer la valeur obtenue à l’ordre de grandeur d’une énergie de votre choix.
|
|
|
|
On
considère que la surace grisée, proche de celle d'un disque de
diamètre D, correspond à la surface de la Soufrière exposée au flux de
muons.
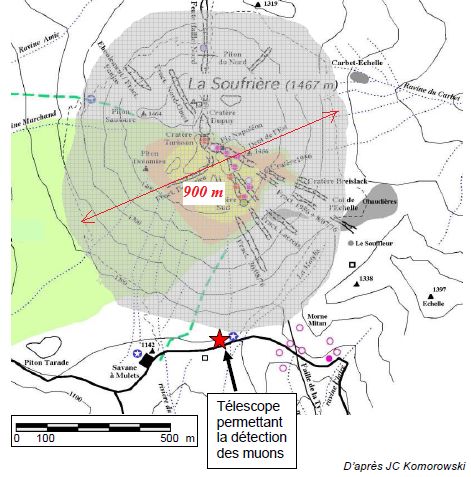
Surface de la Soufrière, disque de diamètre D ~900 m : S = p D2/4 = 3,14 *9002/4 ~ 6,4 105 m2 = 6,4 109 cm2 .
Nombre de muons ordinaires frappant la surface par minute : 6,4 109.
Energie correspondante : 6,4 109 *4 109 =2,6 1019 eV.
ou 2,6 1019 * 1,6 10-19~ 4 J min-1.
Une ampoule de puissance 40 W fonctionnant pendant une seconde consomme une énerge de 40 J.
3.3. Déterminer la valeur du rapport v/c où v est la vitesse d’un muon ordinaire d’énergie 4 GeV. En déduire pourquoi les muons utilisés pour la radiographie
volcanique sont qualifiés d’ « ultra-relativistes ».
Masse d'un muon : m = 105,66 MeV c-2 soit mc2=105,66 MeV.
Energie d'un muon en mouvement : E = g mc2.
g = 4 103 / 105,66 ~38.
1/g2=1-v2 /c2 ~7 10-4 ; v2 /c2 = 1-1/g2= 1-7 10-4 ; v / c ~1,0.
v / c étant supérieur à 0,99, ces muons sont qualifiés d'"ultra-relativistes".
|
|