Performance d'un
athlète. Bac S Polynésie 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
Dans
les parties 1 et 2 de cet exercice, on étudie un lancer de marteau
réalisé par une athlète puis, dans la partie 3, le taux de créatinine
dans le sang de l’athlète.
Étude du mouvement du boulet avant le lâcher du marteau par l’athlète.
Pour simplifier l’étude, on suppose que l’athlète tourne sur elle-même
autour d’un axe immobile vertical et que son bras est toujours tendu.
Dans le référentiel terrestre, le mouvement du boulet est alors supposé
plan et circulaire, accéléré dans un premier temps puis uniforme dans
un deuxième temps.
À partir de la définition du vecteur accélération ar, justifier qualitativement l’existence d’une accélération lors d’un mouvement circulaire.
Le vecteur accélération
est égal à la dérivée par rapport au temps du vecteur vitesse. Dans un
mouvement circulaire, le vecteur vitesse change de direction à chaque
instant, ce n'est pas un vecteur constant au cours du temps et sa
dérivée par rapport à celui-ci n'est pas nulle.
En justifiant la réponse, choisir parmi les schémas ci-dessous, celui
qui correspond à un mouvement circulaire accéléré puis celui qui
correspond à un mouvement circulaire uniforme.
Sur chaque schéma, les vecteurs vitesse et accélération sont
représentés en un point de la trajectoire du boulet en vue de dessus. 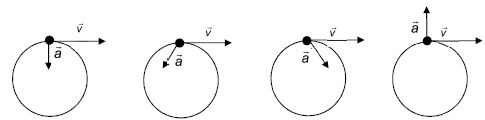
Mouvement circulaire uniforme : l'accélération est centripète ( shéma de gauche).
Mouvement circulaire accéléré : la valeur de la vitesse augmente ( 3è schéma à partir de la gauche).
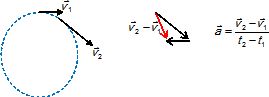
En appliquant la seconde loi de
Newton, justifier le fait que, dans le cas du mouvement circulaire
uniforme, le poids du boulet soit négligeable devant la force exercée
par le câble sur le boulet. La vitesse v est égale à 26 m.s-1, l’intensité de la pesanteur g à 9,8 m.s-2 et le candidat proposera une valeur pour le rayon R de la trajectoire.
Poids du boulet P = mg =4,0 *9,8 =39,2 ~39 N.
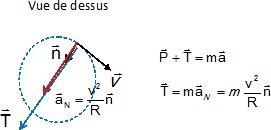
Pour R = 1,5 m : T = 4,0*262 / 1,5 =1,8 103 N, très supérieur au poids.
|
| .
. |
|
|
Étude du mouvement du boulet après le lâcher du marteau par l’athlète.
Le boulet du marteau est assimilé à un point matériel de masse m = 4,0 kg ;
On négligera toute action de l’air ; intensité de la pesanteur : g = 9,8 m.s-2 ;
vitesse initiale du boulet : v0 = 26 m.s-1 ; angle d’envol : a = 45° ;
hauteur du boulet au moment du lâcher : h = 3,0 m.
Pour cette étude, on associe au référentiel terrestre le repère (Ox,
Oz), Oz étant dirigé suivant la verticale ascendante. On négligera dans
cette partie les actions du câble et de la poignée du
marteau. La trajectoire décrite par le boulet dépend de la valeur v0 de la vitesse du boulet au moment de l’envol, de l’angle d’envol a et de la hauteur h du boulet au moment du lâcher à l’instant initial (t = 0). Expression de la trajectoire du boulet.
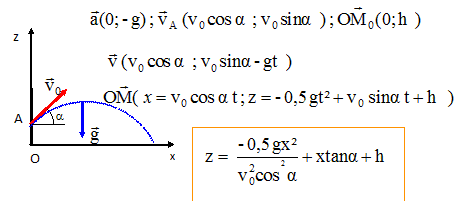
Application numérique : calcul du lancer x lorsque z = 0.
0 = -4,9 x2 /(26*cos45)2 +x tan45 +3,0 ;
0,0145 x2 +x +3,0 = 0 ; D = 1+4*3*0,0145 =1,174 ; D½ =1,0834.
x =(-1 -1,0834) / (-2*0,0145) =71,8 ~72 m. ( Classement 11è).
|
.
|
|
Parmi les trois courbes EP1, EP2 et EP3
représentées s, choisir en le justifiant celle qui correspond à
l’évolution au cours du temps de l’énergie potentielle de pesanteur EP du
boulet pour le lancer effectué par l’athlète entre l’instant initial (t = 0) et l’instant où le boulet touche le sol.
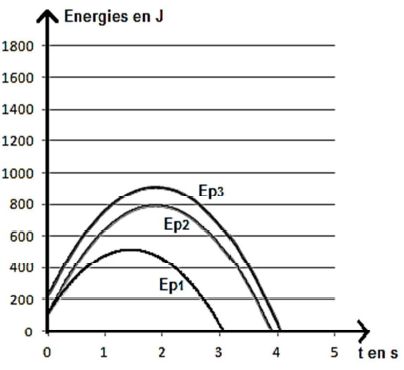
Energie potentielle initiale : mgh = 4,0*9,8*3,0 ~1,2 102 J. ( courbe EP3 exclue ).
Durée du trajet : t = x / (v0 cos a) = 71,8 /(26 cos45) = 3,9 s.( courbe EP2).
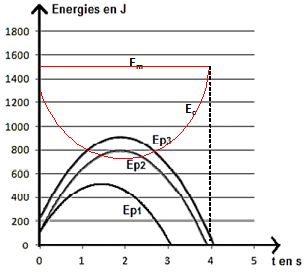
En détaillant votre démarche, représenter sur le graphe, les courbes donnant les énergies cinétique Ec et
mécanique Em du boulet pour le lancer effectué par l’athlète entre l’instant initial (t = 0) et l’instant où le boulet touche le sol.
L'énergie mécanique, somme de l'énergie cinétique et de l'énergie potentielle, est constante.
Energie cinétique initiale : ½mv02 =0,5*4,0*262=1,35 103 J.
Energie mécanique : 1,35 103 +1,2 102 ~1,5 103 J.
Energie cinétique au sommet de la trajectoire : ½m(v0cos 45)2 =0,5*4,0*(26*0,707)2=6,8 102 J.
|
|
Créatine et créatinine chez l’athlète.
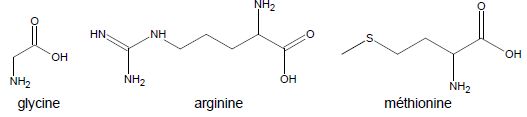
La créatine présente dans le corps peut être d’origine exogène (c’est-à-dire apportée par les aliments) ou endogène (c'est-à-dire synthétisée dans l’organisme) ; sa
synthèse s’effectue alors à partir de trois acides α-aminés : la glycine, l'arginine et la méthionine. La créatine contribue à l’apport en énergie aux cellules musculaires. Les besoins en
créatine sont d’environ 2 g par jour pour un adulte ; il faut cependant
y ajouter 1 à 2 g par jour pour le sportif de forte masse musculaire
qui s’entraîne de manière très intense.
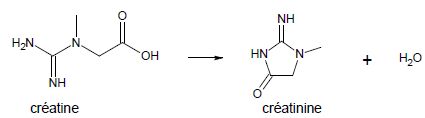
Lors du fonctionnement du muscle, de la créatine se déshydrate
spontanément en créatinine qui passe dans le sang avant d'être filtrée
par les reins et évacuée par voie
urinaire. Bilan de la déshydratation de la créatine :
Le taux de créatinine sanguine est normalement constant dans
l’organisme mais sa valeur dépend de la masse musculaire de l'individu.
Les valeurs attendues dans le sérum sanguin sont chez la femme de 4 à 12 mg.L-1.
Qu’est-ce qui est commun à tous les acides α-aminés ?
Ils possèdent un groupe amine NH2 et un groupe carboxyle COOH portés par le même carbone.
Indiquer, parmi les molécules d’acides α-aminés citées dans le texte, celles qui présentent des énantiomères. Justifier.
L'arginine et la méthionine possédant un atome de carbone asymétrique, présentent des énantiomères.
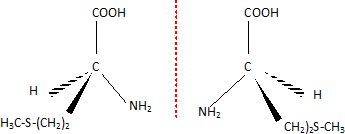
Utiliser la représentation de Cram pour représenter les deux énantiomères de la méthionine.
Déterminer la catégorie de la réaction de déshydratation de la créatine.
Elimination d'une molécule d'eau.
Déterminer la formule brute de la créatinine.
C4H7ON3. M = 4*12+7+16+3*14=113 g/mol.
Dosage du taux de créatinine chez l’athlète.
Pour doser le taux de créatinine dans le sérum sanguin de l’athlète, la méthode de Jaffé, décrite ci-dessous, est utilisée.
La créatinine réagit en milieu basique avec un excès d’acide picrique
pour donner un composé orangé de picrate de créatinine (réaction de
Jaffé). L’intensité de la couleur
obtenue est directement proportionnelle à la concentration de créatinine de l’échantillon.
Dans trois tubes à essais, on réalise les mélanges suivants :
Tube 1 : 1,0 mL d’eau distillée ; 1,0 mL de solution d’hydroxyde de sodium ; 1,0 mL de solution d’acide picrique.
Tube 2 : 1,0 mL de sérum sanguin de l’athlète ; 1,0 mL de solution d’hydroxyde de sodium ; 1,0 mL de solution d’acide picrique.
Tube 3 : 1,0 mL d’une solution de créatinine de concentration C = 100 μmol.L-1 ; 1,0 mL de solution d’hydroxyde de sodium ; 1,0 mL de solution d’acide picrique.
Le contenu de chaque tube est bien agité, puis est laissé au repos pendant 20 minutes.
La mesure de l’absorbance de la solution obtenue dans chacun des tubes
est réalisée avec un spectrophotomètre dont la longueur d’onde est
réglée à 500 nm.
Les résultats sont : A1 =0,00 ; A2 = 0,71 ; A3 = 0,63.
Déduire des résultats du dosage, si le taux de créatinine dans le sang de l’athlète est dans l’encadrement attendu ou non.
L'absorbance et la concentration sont proportionnelles.
c2 = c3A2 / A3=100*0,71 / 0,63 =112,7 ~1,1 102 µmol /L soit 112,7 *113 ~1,3 104 µg/L ou 13 mg/L, valeur supérieure à celle attendue.
Proposer une cause possible d’un taux anormalement élevé de créatinine dans le sang de l’athlète.
Le taux de créatinine
dépend de la capacité d'élimination des reins et de la masse musculaire
importante chez un athlète en plein effort.
|
|
|