Des atomes froids ( ou lents )pour mesurer le temps. Bac S Métropole 2015 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Quelques principes mis en oeuvre dans le refroidissement d’un nuage d’atomes.  Interaction laser - atome de césium au repos. On s’intéresse à un atome initialement immobile dans le référentiel du laboratoire. La quantité de mouvement du système {atome + photon} se conserve. Après absorption d’un photon de quantité de mouvement p = h / l (figure 3.a), l’atome est animé d’une vitesse de « recul » Vrec, de même direction et de même sens que le photon incident (figure 3.b). Dans la situation décrite par les figures 3.a et 3.b, montrer que la valeur de la vitesse de « recul » vrec dans le référentiel du laboratoire, a pour expression : Vrec = h / (lM), avec h la constante de Planck, l la longueur d’onde du laser, et M la masse de l’atome de césium. Calculer la valeur de la vitesse Vrec. La quantité de mouvement  du système {atome + photon } se conserve et l'atome est initialement immobile : h / l = M Vrec ; Vrec = h / (lM) =6,63 10-34 / (852 10-9 *2,207 10-25) =3,53 10-3 m / s. Interaction laser - atome de césium en mouvement dans le référentiel du laboratoire. On restreint l’étude au cas particulier où l’atome de césium est en mouvement dans le référentiel du laboratoire décrit par la figure 5 ci-dessous. La conservation de la quantité de mouvement pour le système {atome+photon} permet d’écrire la relation : h / l-MV = -MV', avec V et V ' vitesses de l’atome respectivement avant et après absorption d’un photon.  Interpréter cette relation en justifiant chacun de ses termes et de ses signes. Exprimer V ' en fonction de V et de Vrec et conclure dans ce cas sur l’effet produit par l’absorption d’un photon sur la vitesse de l’atome de césium. La quantité de mouvement du système { atome + photon} se conserve. Projeter cette relation vectorielle sur un axe horizontal oerienté à droite. 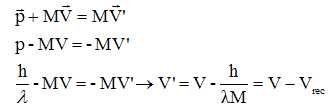Le premier terme correspond à la quantité de mouvement du photon avant absorption ; le second correspond à la quantité de mouvement de l'atome avant absorption ; le dernier correspond à la quantité de mouvement du système après absorption. L’absorption d’un photon se fait sur une durée de l’ordre de Dt = 30 ns pour l’atome de césium. Calculer l’ordre de grandeur de l’accélération subie par cet atome lors de l’absorption d’un photon. Le comparer à l’accélération de cet atome en chute libre. a=(V'-V) / Dt = -Vrec / Dt = -3,53 10-3 / ( 30 10-9)= -1,2 105 m s-2. Cette valeur est 104 fois plus grande que l'accélération de chute libre. . . Le piège magnéto-optique (PMO). Dans le PMO, les six faisceaux laser sont disposés par paire selon trois directions orthogonales de l’espace. Par paire, selon une direction, ils se propagent dans des sens opposés. On considère un atome de césium de vitesse V dans le référentiel du laboratoire en interaction avec une paire de faisceaux laser de fréquence n. On se place dans le cas où l’atome de césium se rapproche du laser de gauche, tandis qu’il s’éloigne du laser de droite comme illustré sur la figure. Dans le référentiel lié à l’atome, les fréquences des deux faisceaux laser perçues par l’atome de césium sont différentes. Quel est le phénomène mis en jeu ? Comparer chacune des deux fréquences perçues par rapport à la fréquence n. Récepteur et émetteur sont en mouvement relatif. Par effet Doppler, la fréquence perçue du photon de gauche est plus grande ( photon et atome se rapprochent ) et la fréquence perçue du photon de droite est plus faible ( photon et atome s'éloignent).  Pour obtenir un ralentissement de l’atome de césium dans la situation de la figure 5, indiquer le photon (gauche ou droite) qui doit être absorbé par l’atome en mouvement. D'après la figure 5, pour obtenir un ralentissement, atome et photon doivent se propager en sens contraire. Le photon de gauche doit être absorbé. Les atomes de césium sont ralentis au centre de six faisceaux laser. On définit la fréquence de résonance atomique par  n12 =( E2-E1) / h, où E1 et E2 sont les énergies des deux niveaux d’énergie de l’atome de césium mis en jeu. La probabilité pour un atome de césium d’absorber un photon d’un faisceau laser est d’autant plus grande que la fréquence du faisceau perçue par l’atome est proche de la fréquence de résonance atomique. Parmi les propositions ci-dessous choisir celle qui convient et la justifier. Pour obtenir un ralentissement efficace des atomes de césium, la fréquence n des lasers est réglée de sorte que : a. n est égale à n12 . b.  n est légèrement inférieure à n12 . c.  n est légèrement supérieure à n12 . Le photon de gauche doit être absorbé. La fréquence perçue du photon de gauche est légèrement plus petite que n12 . Proposition b. Principe de la fontaine de césium. Lorsqu’un atome de césium passe dans la cavité à micro-ondes, il est excité par le rayonnement produit dans la cavité. Ce rayonnement a la même fréquence que celle associée à la transition hyperfine de l’atome de césium. Justifier le terme « micro-ondes » attribué à la cavité. Fréquence de la transition hyperfine de l’atome de césium : 9193 MHz ; longueur d'onde correspondante : 3,00 108 /(9193 106)~ 3,3 10-2 m~3,2 cm. On suppose qu’à l’instant t = 0, le nuage atomique dans l’enceinte sous vide est à l’altitude z = 0. Il est lancé vers le haut avec une vitesse initiale V0 = 5,0 m.s-1. 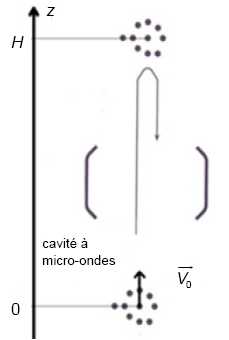Montrer que la date tmax à laquelle le nuage d’atomes atteint le sommet de la fontaine a pour expression : tmax = V0 / g. En déduire l’expression de la hauteur H de la fontaine : H = V02 /(2g). Calculer les valeurs de tmax et de H puis vérifier la cohérence de ces valeurs avec le texte introductif. Dans l'enceinte sous vide, l'atome est en chute libre verticale avec une vitesse initiale V0 orienté vers le haut. V = -g t +V0 ; à tmax, V=0 et tmax =V0 / g = 5,0 / 9,8 = 0,51 s. La position est une primitive de la vitesse  et l'altitude initiale est nulle : z = -½gt2 +V0t. H = -½gt2max +V0tmax = -4,9 *0,512 +5,0 *0,51 = -1,2755 +2,55 ~1,3 m. Les atomes poursuivent leur mouvement vers le haut en ralentissant sous l’effet de la pesanteur et retombent en traversant une deuxième fois la cavité à micro-ondes. Le temps séparant les deux passages par la cavité à micro-ondes est voisin de 2*0,51 ~1,0 s. Ces valeurs sont en accord avec la phrase :" Avec une fontaine haute de un mètre, ce temps est de l’ordre de la seconde, ce qui est cent fois plus qu’avec un jet atomique conventionnel." Des expériences de refroidissement ont été conduites en 1992 par les physiciens de l’ENS (École normale supérieure) en collaboration avec le CNES (Centre national d’études spatiales), lors d’une série de vols paraboliques en avion permettant de se placer dans les conditions de gravité réduite. Dans quel but ces expériences ont-elles été menées ? Justifier votre réponse. Les horloges à fontaine atomique de césium sont des horloges parmi les plus précises à ce jour. La précision de ce type d’horloge est d’autant plus grande que le temps séparant les deux passages par la cavité à micro-ondes est grand. tmax = V0 / g. En microgravité, g est très faible et à V0 constant, tmax est très grand.

menu