Micro-texturation
de surface par un laser femtoseconde.
Bac S Métropole, Réunion 2015
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
|
|
|
|
|
La
micro-texturation de surface est une technologie qui permet d’optimiser
la lubrification des pièces métalliques en contact, par exemple dans
les moteurs employés dans les sports mécaniques (formule 1, moto grand
prix, etc.). Cette micro-texturation est réalisée sur des matériaux
appelés DLC (Diamond Like Carbon) déposés en fines couches sur les
pièces à
lubrifier. Grâce à l’utilisation d’un laser à impulsions
ultra-brèves, on crée à la surface des pièces mécaniques un réseau de
motifs (cavités, rainures, etc.) ayant des dimensions de quelques
dizaines de micromètres qui se comportent comme des microréservoirs
d’huile (après lubrification).
À
la différence d’un laser conventionnel qui produit un rayonnement
continu, les lasers pulsés émettent des flashs lumineux très brefs
qu’on appelle des impulsions. La durée t et la cadence (fréquence) f de
ces impulsions sont réglables. Un laser pulsé est dit « femtoseconde » si la durée t est de l’ordre d’une à quelques
centaines de femtosecondes. Contrairement aux lasers continus qui
produisent un rayonnement monochromatique, les lasers pulsés émettent
un rayonnement polychromatique dans une bande de fréquence de largeur Dn centrée sur une fréquence n0.
Les énergies des impulsions femtosecondes peuvent paraître faibles (de
l’ordre du mJ à f = 1 kHz) mais leur brièveté fait que la puissance
instantanée du laser durant une impulsion (puissance de crête) peut
atteindre plusieursgigawatts dans le domaine industriel.
Cavité de diamètre D et de profondeur p dans une couche de DLC.
Lorsqu’on
dirige un faisceau laser pulsé femtoseconde vers une surface recouverte
de DLC, chaque impulsion laser apporte suffisamment d’énergie pour
graver (creuser) une cavité cylindrique dans la couche de DLC.
On admet que le diamètre de la cavité gravée correspond au diamètre D du faisceau laser utilisé.
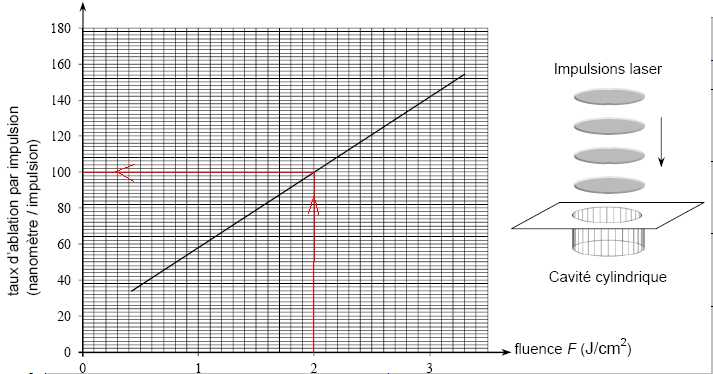
On a tracé ci-dessous la courbe donnant le taux d’ablation du DLC par impulsion, c'est-à-dire la
profondeur
de la cavité gravée par une seule impulsion laser, en fonction de la
fluence F du laser utilisé. La fluence est obtenue en divisant
l’énergie d’une impulsion laser (en J) par la surface circulaire gravée
(en cm2).
On
admettra, comme le montre les schémas ci-dessous, que la profondeur
totale p de la cavité gravée est proportionnelle au nombre d’impulsions
reçues et donc à la durée Dt de la gravure.
|
| .
. |
|
|
Domaine d’émission du laser femtoseconde.
Le laser femto seconde présenté est dit « infrarouge ». Justifier.
Fréquence centrale du rayonnement émis f0 =375 THz = 3,75 1014 Hz.
l = c / f0 =3,00 108 / (3,75 1014) = 8,0 10-7 m = 800 nm.
Cette valeur étant supérieure à 780 nm, le laser émet dans le proche infrarouge.
Ce laser apparaît rouge à l’observateur. Justifier.
Largeur de la bande de fréquence : Dn = 100 THz.
Longueur d'onde minimale : l mini = c / fmaxi =3,00 108 / (4,25 1014) = 7,0 10-7 m = 700 nm.
Gamme de longueur d'onde correspondant aux radiations rouges 620 à 780 nm.
Caractéristiques d’une impulsion du laser femtoseconde.
Montrer que l’énergie transportée par une seule impulsion du laser précédent est égale à 0,15 mJ.
Puissance crète atteinte durant une impulsion fois durée d'une impulsion :
Pcrète t = 1,0 109 *150 10-15 =1,5 10-4 J = 0,15 mJ.
Évaluer le nombre de photons produits par le laser durant une seule impulsion.
Energie moyenne d'un photon E = h f0 =6,63 10-34 *3,75 1014 =2,486 10-19 J.
Nombre de photons émis par impulsion : 1,5 10-4 / (2,486 10-19)=6,0 1014.
|
.
|
|
Gravure par le laser femtoseconde.
On utilise le laser femtoseconde pour graver une cavité dans une couche de DLC.
Déterminer la fluence du laser étudié, puis la durée Dt nécessaire à la gravure d’une cavité circulaire cylindrique de 98 μm de diamètre et de 6 μm de profondeur.
La fluence est obtenue en divisant l’énergie d’une impulsion laser (en J) par la surface circulaire gravée (en cm2).
F = 1,5 10-4 /(3,14 *(49 10-4)2)=1,99 104 ~2,0 J cm-2.
Le
taux d'ablation est de 100 nm par impulsion. il faut donc 6000 / 100=
60 impulsions pour graver une cavité cylindrique de 6 µm de profondeur.
Durée de la gravure : 60 *période des impulsions =60 * 1,0 = 60 ms.
.
|
|