QCM physique. Concours Paces Lyon
2013
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Viscosité.
Les vecteurs sont écrits en gras et en bleu.
La force de frottement F d'une sphère de rayon r se déplaçant à la vitesse v dans un fluide de coefficient de viscosité h est : F = -6p r h v.
A- L'unité SI du coefficient de viscosité est Pa s-1. Faux.
B- L'unité SI du coefficient de viscosité est Pa s. Vrai.
C- L'unité SI du coefficient de viscosité est kg m-1 s-1. Vrai.
D- La dimension du coeficient de viscosité est ML-1T-1. Vrai.
E- La dimension du coeficient de viscosité est MLT2. Faux.
Marche pieds nus.
Dans une pièce à 20 °C, la sensation de froid provoquée par une personne marchant pieds nus sur un sol carrelé ( l = 1 W m-1 K-1) par rapport à sa sensation sur un tapis ( l = 0,04 W m-1 K-1), s'explique par :
A- La température du carrelage est inférieure à celle du tapis. Faux.
B- Le transfert de chaleur par conduction est plus efficace sur le carrelage. Vrai.
Le carrelage est meilleur conducteur que le tapis l carrelage = 25 fois l tapis.
C- la différence de température du carrelage entraîne une
vasoconstriction réflexe des pieds qui suffit à elle seule à expliquer
cette sensation de froid. Faux.
D- Le transfert d'énergie par convection est plus grand sur le carrelage. Faux.
E- Le coefficient de conductivité thermique est 25 fois moins élevé sur le carrelage que sur le tapis. Faux.
Modèle du gaz parfait.
A. Le modèle du gaz parfait prend en compte les interactions moléculaires. Faux.
B- L'énergie interne d'un gaz parfait monoatomique est la somme des énergies cinétiques de translation des atomes. Vrai.
C- A haute température, l'énergie interne d'un gaz parfait moléculaire
est la somme des énergies cinétiques de translation des
molécules. Faux. L'énergie
interne est la somme de l'énergie cinétique du centre de masse des
molécules et de l'énergie interne des molécules ( vibration, rotation ).
D- Le modèle du gaz parfait décrit correctement le comportement des gaz réels aux hautes pressions. Faux.
Ce modèle du gaz parfait décrit le comportement des gaz réels aux basses pressions.
E- L'énergie interne d'un gaz parfait monoatomique est proportionnelle à la température. Vrai.
Radioactivité.
L'activité d'une source radioactive est de 1 MBq au début de
l'expérience. Elle n'est plus que de 62,5 kBq le lendemain à la même
heure. On donne 100 /6,25 = 16 ; ln2 ~0,69 et e -1 = 0,37. A- La période radioactive ou demi-vie correspond au temps nécessaire à la disparition de la moitié des noyaux radioactifs. Vrai.
B- La durée de vie moyenne est l'intervalle de temps moyen au bout
duquel il ne reste que 10 % des noyaux initialement présents. Faux.
Demi-vie t½ = ln2 / l et durée de vie moyenne =1/l.
C- Le becquerel ( Bq) est l'unité SI utilisée pour exprimer l'activité et correspond à une désintégration par seconde. Vrai.
D- La période radioactive est de 6 heures. Vrai.
En 24 heures l'activité est divisée par 16 = 24. 24 h = 4 t½ ; t½ = 6 h.
E- La période radioactive est 1 h 30 min. Faux.
Forces électromagnétiques.
A- La force de Lorentz résulte des effets conjoints d'un champ électrique et magnétique. Vrai.
B- La force de Laplace est proportionnelle à l'intensité du courant qui lui donne naissance. Vrai.
C- L'effet hall permet de mesurer le champ magnétique produit par un courant circulant dans un fil linéaire. Vrai.
D- La loi de Biot et Savart s'applique uniquement au calcul du champ magnétique d'une bobine circulaire. Faux.
E- La loi de Lenz exprime que le courant induit par induction magnétique s'oppose aux causes qui lui ont donné naissance. Vrai.
Optique géométrique. 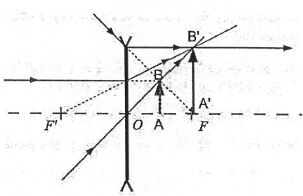
A- La lentille est divergente. Vrai.
B- L'objet est réel. Faux. Un objet réel est situé à gauche de la lentille.
C- L'objet est virtuel. Vrai.
D- L'image est réelle. Vrai. Elle est située à droite de la lentille.
E- L'image est virtuelle. Faux.
|
|
|
RMN.
A- Le phénomène RMN permet d'étudier tous les noyaux. Faux. Les noyaux doivent posséder un spin nucléaire.
B- Le signal RMN d'un proton dépend du champ magnétique B0 dans lequel il est placé. Vrai.
C- La polarisation des spins par le champ B0 place les spins sur deux niveaux d'énergie séparés par une différence d'énergie DE = g h B0. Faux. DE = ghB0/(2p).
D- D'après la loi de Boltzmann, on peut
augmenter la différence de répartition des spins entre deux niveaux
d'énergie en baissant la température de l'échantillon. Faux.
E- Pour enregistrer un signal RMN, il faut d'abord exciter les spins avec un deuxième champ magnétique B1 de même direction que B0. Faux. Les noyaux sont placés dans un champ magnétique externe et excités par un rayonnement radiofréquence.
Effets biologiques des radiations ionisantes.
A- Les effets obligatoires ( déterministes) se caractérisent par un seuil en-dessous duquel ils ne sont jamais observés. Vrai.
B- Les effets déterministes ont une gravité augmentant avec la dose. Vrai.
C- Les effets aléatoires ( stochastiques) sont irréversibles. Faux.
D- Les effets aléatoires sont de gravité proportionnelle à la dose. Faux.
E- Les effets aléatoires incluent des cancers et des mutations génétiques. Vrai.
Transformations radioactives.
A- L'émission ß+ provient d'une transformation isobarique. Vrai.
B- L'émission d'un ß- est toujours accompagnée de l'émission d'un neutrino. Faux.
L'émission d'un ß- est toujours accompagnée de l'émission d'un anti-neutrino.
C- Lors de la désintégration a, l'énergie cinétique du "noyau de recul " est égale à l'énergie cinétique de la particule a émise. Faux. La particule a emporte près de 98 % de l'énergie disponible.
D- lors de l'émission ß+, un proton se transforme en neutron. Vrai.
E- L'émission d'un photon g est liée à un phénomène de désexcitation atomique. Vrai.
Analyse dimensionnelle.
La fréquence f de vibration d'une étoile peut être exprimée en fonction de son rayon R, de sa masse volumique r et de la constante de gravitation G par la relation : f = kRa rb Gc. k est une constante sans dimension. La dimension de G est [G]=M-1L3T-2.
Les valeurs numériques des exposants sont :
A- a = ½ ; b = -½ ; c = ½. Faux.
[f]= T-1 ; [R]= L ; [r] = M L-3 ; [f] = La Mb L-3b M-cL3cT-2c = Mb-cLa-3b+3cT-2c ;
par identification : c = ½ ; b = ½ ; a = 0.
B- a = 0 ; b = ½ ; c = ½. Vrai.
C- a = -1 ; b = -½ ; c = ½. Faux.
D- a = 0 ; b = ½ ; c = -½. Faux.
E- a = ½ ; b = -½ ; c = -½. Faux.
Calorimétrie.
Dans un calorimètre parfaitement isolé contenant 200 g d'eau à 20°C, on introduit un glaçon de m =50 g à 0°C. Ceau = 4200 J K-1 kg-1 ; L fusion glace = L = 300 kJ kg-1.
A- La température finale est 5°C. Faux.
Hypothèse : toute la glace fond et l'eau de fonte se réchauffe.
Energie nécessaire à la fonte totale de la glace Q1 = 0,050*300 = 15 kJ ;
Energie gagnée par l'eau de fonte : m Ceau qfin =0,050*4,200 qfin =0,21 qfin kJ.
Energie cédée par l'eau chaude : 0,200 *4,200*(qfin-20) =0,84 qfin -16,8.
Système adiabatique : 15+0,21qfin + 0,84 qfin -16,8 = 0
1,8 = 1,05 qfin ; qfin =1,7°C.
B - la température finale est 5 K. Faux.
C- Le glaçon n'a pas fondu à l'équilibre. Faux.
D- 15000 J sont nécessaire pour la fonte du glaçon. Vrai.
E- La température finale est 0°C. Faux.
|
.
|
|
Incertitude de mesure.
On détermine la viscosité h d'un liquide à l'aide d'un viscosimètre à chute de bille. h = K(rs-r) t. On néglige l'incertitude sur la constante K ; rs est la masse volumique de la bille ; r est la masse volumique du liquide et t le temps de chute de la bille. L'incertitude de mesure de la viscosité est donnée par :
Prendre la dérivée logarithmique :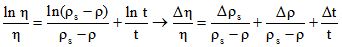
Spectroscopie optique.
Un atome a des niveaux d'énergie électronique donnés par E(n) = -32 / n2 avec E(n) en eV et n nombre quantique principal. On prendra hc/e = 1,2 10-6 SI.
Le photon émis lors de la transition directe du niveau 4 au niveau 2 est :
A- dans l'ultraviolet. Vrai.
E4 =-32 / 16 = -2 eV ; E2 = -32 / 4 = -8 eV ; DE = 6 eV = 6 *e J.
DE =hc/l ; l = hc/(6 e) =1,2 10-6 / 6 = 2 10-7 m = 200 nm ( domaine UV).
B- Dans le visible. Faux.
C- dans l'infrarouge. Faux.
D- De longueur d'onde dans le vide 200 nm. Vrai.
E- De fréquence 5 1014 Hz. Faux.
f =c/l=3 108 / (2 10-7) =1,5 1015 Hz.
Loi de Beer-Lambert.
Le tableau ci-sdessous donne l'intensité lumineuse transmise I1 à travers une cuve contenant une solution de concentration 1 mmol/L en fonction de l'épaisseur L de la cuve.
L(cm)
|
0
|
1
|
2
|
3
|
4
|
5
|
I1 ( unité arbitraire)
|
I0=75
|
0,075
|
7,5 10-5
|
7,5 10-8
|
7,5 10-11
|
7,5 10-14
|
-log ( I1/ I0)
|
0
|
3
|
6
|
9
|
12
|
16
|
-log ( I1/ I0) / L
|
|
3
|
3
|
3
|
3
|
3
|
Le coefficient d'extinction molaire en L mol-1 cm-1 est 3, 30, 300, 3000, 30 000.
I1 = I010(-eLc ) ; log ( I1/ I0) = -eL c ; -log ( I1/ I0) / L = e c avec c = 10-3 mol/L ; e = 3 103 L mol-1 cm-1.
Désintégration radioactive.
Le 64Cu se désintègre par capture électronique CE, soit par émission ß+ ou par émission ß-.
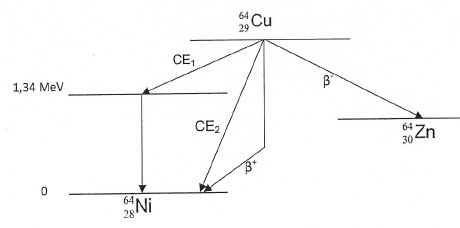
On donne m(6429Cu-m(6430Zn)=0,6 10-3 u, m(6429Cu-m(6428Ni)=1,8 10-3 u, 1u = 931,5 MeV /c2 et la masse de l'électron me = 0,511 MeV/c2.
A- L'énergie maximale emportée par la particule ß- est 0,56 MeV. Vrai.
6429Cu ---> 6430Zn +0-1e.
Dm = mnucléaire(6430Zn) +me-mnucléaire(6429Cu)=matomique(6430Zn) -matomique(6429Cu) =-0,6 10-3u =-0,6 10-3*931,5 = -0,56 MeV/c2.
B- L'énergie maximale emportée par la particule ß+ est 1,68 MeV. Vrai.
6429Cu ---> 6428Ni +01e.
Dm = mnucléaire(6428Ni) +me-mnucléaire(6429Cu)= matomique(6428Ni) -matomique(6429Cu)=-1,8 10-3u =-1,8 10-3*931,5 =-1,68 MeV/c2.
C- On peut observer des photons d'énergie 1,34 MeV et 0,511 MeV. Faux.
CE2 : 6429Cu +0-1e ---> 6428Ni.
D- Le noyau de zinc 64 compte 36 neutrons. Faux. 64-30 = 34 neutrons.
E- Le cuivre 64 et le nickel 64 sont isotones. Faux.
Isotone signifie même nombre de neutrons . Le cuivre 64 possède 64-29 = 35 neutrons et le nickel 64 en possède 64-28 = 36.
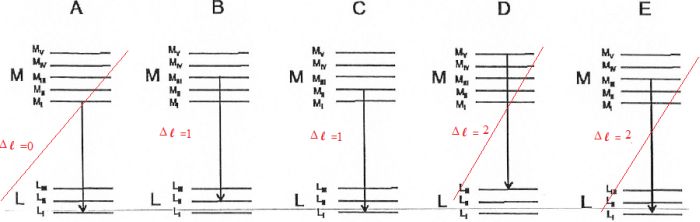
Raies X caractéristiques.
Quelles sont les transitions électroniques permises entre les niveaux M et les niveaux L ?
Les transitions permises correspondent à Dl = ±1.
Interférences.
En un point M d'un écran interfèrent 4 ondes électromagnétiques
déphasées de polarisation rectiligne, dont la direction de
polarisation, la fréquence et l'amplitude sont identiques. Leurs champs
électriques en M sont : E1 = E0 cos (wt) ; E2 = E0 cos (wt+½p) ; E3 = E0 cos (wt+p) ; E4 = E0 cos (wt+1,5p) ; on note I1 = <E12> l'intensité de la première onde.
L'intensité totale en M vaut : 0 ; I1 ; 2I1 ; 4I1 ; 8 I1.
<E12> = <E02> <cos2 (wt)>= ½<E02> ; E2 = E0 cos (wt+½p) = E0 sin (wt) ; <E22> = <E02> <sin2 (wt)>= ½<E02> ;
E3 = E0 cos (wt+p) = -E0 cos (wt) ; <E32> = <E02> <cos2 (wt)>= ½<E02> ;
E4= E0 sin (wt+1,5p) = -E0 cos (wt) ; <E42> = <E02> <cos2 (wt)>= ½<E02> ; IM =2 I1.
|
|
|
Modes d'un laser.
Le milieu amplificateur d'un laser de cavité de longueur L = 1,5 mm a
un gain dépassant les pertes pour les fréquences entre 5 1014 Hz et 5,1 1014 Hz.
Le nombre de modes de ce laser est environ : 1 ; 10 ; 100 ; 1000 ; 10 000.
Ecart entre deux modes longitudinaux consécutifs : Dn = c/2L =3 108 / (3 10-3) = 1,0 1011 Hz.
5,1 1014 -5,1 1014 =1,0 1013 Hz ; 1,0 1013 / (1,0 1011)=100.
Transformation isobare.
Soit un système constitué d'un récipient fermé par un piston
mobile de masse négligeable qui peut bouger sans frottement le long des
parois. Il contient une mole de gaz monoatomique parfait dans un
volume 1 L et se trouve à la pression p = 1 bar constante au
cours de la transformation. On chauffe lentement le récipient jusqu'à
ce que le volume atteigne 2 L.
A- Le travail mis en jeu par le système vaut W = 200 J. Faux
W12 = -P(V2-V1) =-105 (2-1)10-3 = -100 J.
B- La variation de l'énergie interne du système est DU = 150 J. Vrai.
DH=gRDT/(g-1) avec g = 5/3 ; DH=2,5 R DT.
PV1=RT1 ; PV2=RT2 ; R DT = P(V2-V1)=100 ; DH=Q=2,5*100 = 250 J.
DU = Q+W =250-100 = 150 J.
C- La transformation est adiabatique. Faux. Le système reçoit de la chaleur.
D- La chaleur reçue par le système vaut 250 J. Vrai.
E-
Si la masse du piston n'est plus négkigeable et que sont mouvement est
vertical, alors la pression à l'intérieur du récipient est différente
de celle de l'extérieur. Vrai.
Dipôles électrostatiques.
Les vecteurs sont écrits en gras et en bleu.
Deux dipôles A ( de centre O) et B( de centre O') de longueur l et de moments dipôlaires électrostatiques pA et pB ( colinéaires et de sens opposés) sont placés dans le vide.
Ils sont éloignés l'un de l'autre de la distance R =OO' >> l.
On appelle E(A) le champ électrique créé en O ' par le dipôle A et E(B)
le champ électrique créé en O par le dipôle B. On rappelle que la norme
du champ électrique créé par un dipôle, de centre O de moment dipolaire
de norme p, en un point M quelconque de l'espace situé à une distance r
>> l est :
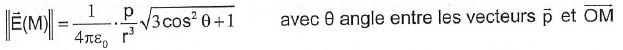
A- E(A) et E(B) sont de sens contraire. Vrai.
En rouge, champ créé en O' par la charge q ; en vert champ créé en O' par la charge -q ; en noir champ total en O'.

En rouge, champ créé en O par la charge q ; en vert champ créé en O par la charge -q ; en noir champ total en O.

B- E(A) et E(B) sont de même sens. Faux.
C- La norme de E(B) est égale à 1/(2pe0) pB/R3. Vrai.
Dans l'expression du champ donnée ci-dessus, cos q =cos0 = 1.
D- L'énergie potentielle du dipole A est égale à -pA /(2pe0) pA/R3. Faux.
Ep = -pA. E(B) = pA/(2pe0) pB/R3.
E- L'énergie potentielle d'interaction électrostatique entre les deux dipôles est égale à -pA /(pe0) pB/R3. Faux.
Ondes stationnaires.
L'équation d'onde admet pour solution Y = B sin (kx+f) sin (wt+F) dans le cas d'une onde stationnaire.
Soit une onde stationnaire dont le champ électrique est polarisé
suivant Oz et se propageant selon Ox dans le vide. Elle est confinée
entre deux miroirs métalliques séparés par une distance L et vérifie
l'équation d'onde.
On a pour tout t : ||E(t, x=0)||=0 et ||E(t, x=L)||=0.
Les solutions sont ( avec n entier positif) :
Y(x=0) =B sin (f) sin (wt+F) = 0 ; d'où f = 0.
Y(x=L) =B sin (k L) sin (wt+F) = 0 ; d'où k = np/L.
Le champ électrique est polarisé suivant Oz : En =B sin (np/L x) sin (wt+F) uz avec w = kc = np/L c.
E- Pour n >3, la distance entre deux maxima du champ électrique est : 2 L/n. Faux.
E(n) présente un maximum si np/L x = (2k+1)½p ; pour k = 0 : x1 =L /(2n) ; pour k = 1 : x2 =3L /(2n) ; x2-x1 =L/n.
Tube à rayons X.
On considère un tube à rayons X à anode de chrome, fonctionnant sous
une tension U = 12,4 kV. Les énergies d'ionisation des niveaux K, LI et LII du chrome sont respectivement EiK =6,2 keV, EiLI =0,7 keV et EiLII =0,6 keV. On prendra hc/e = 1,24 10-6 SI.
A- On peut observer sur le spectre d'émission de la raie X d'énergie
5,5 keV correspondant à la transition électronique entre les niveaux LI et K du chrome. Vrai.
EiK-EiLI =6,2-0,7 = 5,5 keV.
B- L'énergie d'un photon correspondant à la raie Ka2 est de 5,6 eV. Vrai.
Transition du niveau LII au niveau K : DE =6,2-0,6 =5,6 eV.
C. L'énergie maximale du rayonnement de freinage est 12,4 keV. Vrai.
On admet que certains électrons sont arrêtés brutalement dans l'anticathode. En admettant que leur énergie est intégralement convertie en énergie de rayonnement X, l'énergie du rayonnement X : E= hc/l0 = eU.
D- Le maximum d'intensité du rayonnement de freinage est observé pour une énergie d'environ 8,3 keV. Vrai.
On rappelle que les photons les plus probables ont pour longueur d'onde lm = 1,5 l0 ; Emaxi =eU/1,5 = 12,4 / 1,5 =8,3 keV.
E- La longueur d'onde minimale du rayonnement de freinage est l0 = 1 nm. Faux.
l0 =hc / (eU)=1,24 10-6 /(12,4 103)=1,0 10-10 = 0,1 nm.
OEM polarisation.
Une onde électromagnétique polarisée horizontalement traverse successivement trois polarisuers :
- le premier avec un axe incliné de 60 ° ( sens trigonométrique ) par rapport à l'horizontale.
- le second avec un axe incliné de 120 ° ( sens trigonométrique ) par rapport à l'horizontale.
- le troisième avec un axe horizontal.
On donne cos 60 = ½.
Le rapport entre les intensités à la sortie et à l'entrée de l'ensemble des polariseurs est : 1, 0,25, 1/16, 1/64, 0.
L'intensité lumineuse I qui émerge d'un polariseur en fonction de l'intensité I0 qui entre est : I = I0 cos 2 a.
I1 = I0 cos 2 60 = 0,25 I0 ; I2 = I1 cos 2 120 =0,25 I1 =I0/16 ; I3 =I2 cos 2 0 =I2 =I0/16.
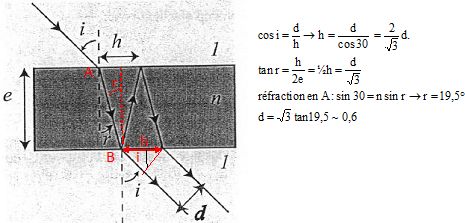
Propagation d'un rayon lumineux à travers une lame de verre. nverre = n = 1,5.
Dans le cas où i = 30° et e = 1 cm la distance d est ( en cm) : 2 ; 1 ; 0,6 ; 0,2 ; 0,1.
|
|