Echolocalisation des chauves -souris.  Concours orthoptie Montpellier 2014. En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . L’écholocalisation des chauves-souris. Doc.1 Les cris - On classe les cris ultrasonores des chauves-souris en trois groupes : les émissions de fréquence constante (FC), les émissions de fréquence modulée décroissante (FM) et les émissions mixtes (FC-FM). En général, ces ultrasons ne sont pas purs mais composés d’une fréquence fondamentale et de plusieurs harmoniques Pour qu’une proie soit détectable, elle doit avoir une dimension supérieure à la longueur d’onde du signal ultrasonore. Détection des distances - Pour estimer la distance à un objet (obstacle fixe, proie…), les organes sensoriels de la chauve-souris enregistrent le retard de l’écho par rapport à l’émission du signal. Détection de la vitesse – La chauve-souris perçoit sa vitesse relative par rapport à un objet grâce au décalage de fréquence du signal réfléchi dû à l’effet Doppler. Les battements d’aile d’une proie produisent un décalage des fréquences par effet Doppler oscillant qui se superposent au décalage général engendré par les obstacles fixes environnants. Chez certaines espèces, pour faciliter la détection de ces oscillations, il existe un système de compensation : ces espèces modifient la fréquence d’émission pour que la fréquence du signal réfléchi par les obstacles fixes soit ramenée à une fréquence de référence, celle qui est émise lorsque la chauve-souris est immobile, et pour laquelle la sensibilité est maximale. Donnée : Vitesse du son (ou des ultrasons) dans l’air : vson = 340 m.s-1. Qu’appelle-t-on « cris ultrasonores » ? Il s'agit d'un ensemble de sons brefs dont les fréquences sont supérieures à 20 kHz ( domaine des ultrasons). Est-ce une onde longitudinale ou transversale ? Justifier. Une onde ultrasonore est une onde mécanique longitudinale : la direction de la perturbation ( variation de pression de l'air ) est la même que la direction de propagation de l'onde. À partir du Doc.2, déterminer la période T des signaux émis par les chauves-souris. 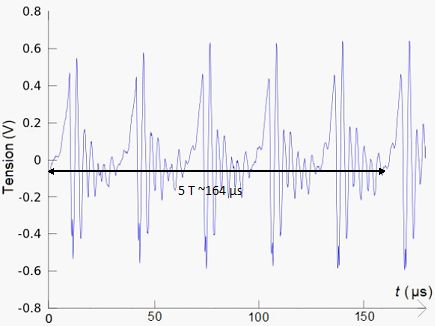T= 164/5 ~33 µs = 3,3 10-5 s. En déduire la fréquence fondamentale f des signaux émis par les chauves-souris. Conclure. f = 1/T = 1/(3,3 10-5) ~30 kHz ; ces cris appartiennent  bien au domaine des ultrasons. Quelle est la fréquence de ses deux harmoniques les plus proches ? Les fréquences des harmoniques sont des multiples de la fréquence du fondamental ; donc 60 kHz, 90 kHz ... Nommer le phénomène qui perturbe la détection d’un écho pour que la proie soit détectable. La diffraction de l'onde par une proie dont les dimensions sont de l'ordre de grandeur de la longueur d'onde des cris. Calculer la dimension minimale d’une proie pour qu’elle soit détectable. La taille de la proie doit être supérieure à 3 fois la longueur d'onde. l = vson / f = 340 / (3,3 104) ~1,0 10-2 m ~1,0 cm ; taille minimale de la proie : 3 cm. Réaliser un schéma qui modélise la détection des distances d’une chauve-souris qui se rapproche d’un obstacle fixe. Y faire apparaitre le parcours du signal émis se rapprochant de l’obstacle, puis expliquer comment la chauve-souris peut ainsi estimer les distances. Le signal émis est réfléchi par l'obstacle puis détecté par la chauve souris. Connaissant la durée Dt de l'aller-retour et la célérité du son dans l'air, la distance d peut être calculée 2d = vson Dt. En utilisant le Doc.3, calculer la distance séparant la chauve-souris du mur. 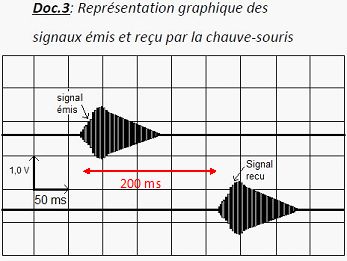d = 340 * (100 10-3) =34 m. Expliquer pourquoi « Les battements d’aile d’un insecte produisent un décalage des fréquences par effet Doppler oscillant ». Les ailes de la proie se rapprochent, puis s’éloignent de la chauve-souris, ce qui génère un décalage Doppler de la fréquence reçue par la chauve-souris ; de plus, ce battement étant périodique, ce décalage oscille entre deux valeurs extrèmes.  Donner un exemple d’utilisation de l’effet Doppler dans le domaine des ondes électromagnétiques. Mesure de la vitesse des véhicules par les radars, détermination de la vitesse d'éloignement des galaxie en astrophysique. . Lorsque la chauve-souris se rapproche d’un mur, l’écho perçu a-t-il une fréquence plus grande, identique ou plus faible que celle du signal émis ? Justifier simplement. La fréquence de l'écho reçu est plus grande que celle du son émis. La distance parcourue par l'onde réfléchie est plus faible ; la longueur d'onde diminue et f = vson / l. La fréquence va donc croître. On propose deux relations pour l’expression de la fréquence perçue fR par une chauve-souris se dirigeant vers un mur à la vitesse de v = 20 km.h-1. On note f0 la fréquence du signal émis. (1) : fR = (vson-v) f0 / (vson + v) ; (2) fR = (vson+v) f0 / (vson - v) ; (3) v = vson Df / (2f0). Laquelle des relations (1) ou (2) est utilisable dans le cas décrit ? Justifier. fR est supérieure à f0 : (2) convient, le numérateur doit être supérieur au dénominateur. Calculer la fréquence fR de l’écho reçu lorsque le signal émis a pour fréquence 62 kHz. v = 20 /3,6 = 5,56 m/s ; fR = (340+5,56) *62 / (340-5,56) ~64 kHz. En utilisant une des expressions précédentes, calculer la vitesse v d’une proie par rapport à la chauve-souris, lorsque celle-ci perçoit un décalage de fréquence Δf = 880 Hz pour un ultrason émis à la fréquence f0 = 93 kHz. v = vson Df / (2f0) = 340*880 /(2*93 103) =1,6 m/s, vitesse relative par rapport à la chauve souris. Combien de temps va mettre la chauve-souris pour rattraper sa proie, supposée située à 8,5 m d’elle en ligne droite ? t = d/vproie) = 8,5 /1,6 = 5,3 s.

menu