Plancher chauffant,
skateboardeur, écholocalisation des chauves -souris. Concours
orthoptie Montpellier 2014.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Question de
cours.
Que
faut-il pour que la troisième loi de Newton s’applique à deux corps A
et B en interaction ?
Les lois de Newton s'applique dans un référentiel galiléen et fondent
la mécanique classique. Pour que la troisième s'applique il faut deux
corps en interaction.
Qu’observe
t-on lorsque l’on réalise des interférences en lumière blanche ?
La
lumière blanche étant polychromatique, chaque radiation donne son
propre système d'interférences qui vont se superposer.
La tache centrale est blanche. De part et d'autre on observe
l'irrisation de la figure d'interférences ( apparition de diverses
couleurs).
Quelle
est la différence entre les forces conservatrices et les forces non
conservatrices? Donnez un exemple pour chacune.
Le travail d'une force conservative est indépendant du chemin suivi par
son point d'application. Si ce n'est pas le cas, elle est dite
non-conservative. La force électrique, la force de gravitation sont
conservatives ; la force de frottement est non-conservative.
Qu’est-ce
que la numérisation ?
La numérisation est la conversion des informations d'un support (
texte, image, son ) en données numériques que des dispositifs
informatiques pourront traiter.
Si
deux instruments identiques produisent chacun en un point un son de
même intensité. Comment sera le niveau sonore global ?
Le niveau sonore augmente de 3 dB, par rapport à un instrument seul,
lorsque les deux instruments identiques produisent chacun un son de
même intensité.
Dans
quel référentiel, le mouvement de Jupiter est circulaire ?
Dans le référentiel héliocentrique, le mouvement de Jupiter est
circulaire.
Qu’est-ce
que l’épicentre d’un séisme ?
L'épicentre est le lieu de la surface terrestre situé à la verticale du
foyer d'un séisme.
Si,
sur le chemin d’une onde lumineuse monochromatique, on place un fil
horizontal d’épaisseur a, on obtient une figure de diffraction de quel
type ?
Le cheveu étant horizontal, la figure de diffraction est verticale.
Quelles
sont les deux sources de rayonnements électromagnétiques qui
transportent le moins d’énergie ?
Plus la longueur d'onde est grande, plus l'énergie transportée par
l'onde est faible : ondes radio,ondes radar, micro-ondes.
Le
code RVB « 255 ; 0 ; 255 » correspond à un pixel magenta, jaune ou cyan
?
Le vert est absent, seuls le rouge et le bleu sont présents avec la
même intensité. Le pixel correspond au magenta.
Plancher
chauffant.
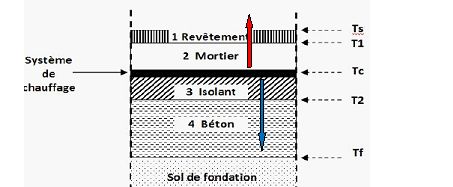
La figure ci-dessous représente la coupe transversale d’un plancher
dans lequel on a incorporé un système de chauffage. Ce système est
constitué d’un tube dans lequel circule de l’eau à la température
moyenne supposée constante T c = 40°c. On assimile le
système de chauffage à un plan horizontal à la température uniforme de T c
= 40°C.
On note T s = 24°C et T f = 7°C respectivement la
température du local et la température du sol de fondation.
Matériaux
|
Indice
|
Conductivité
thermique l ( W m-1
K-1)
|
Epaisseur
(cm)
|
Revêtement
|
1
|
2,50
|
1
|
Mortier
|
2
|
1,15
|
5
|
Isolant
|
3
|
0,02
|
2
|
Béton
|
4
|
1,40
|
10
|
Représenter
sur le schéma ci-dessus le sens des flux thermiques circulant dans le
plancher chauffant.
Indiquer
le mode de transfert de chaleur.
Le transfert s'effectue par conduction, du corps le plus chaud vers le
corps ( le système de chauffage ) le plus froid ( vers la pièce
et vers le sol).
Calculer
les résistances équivalentes de part et d’autre du système de chauffage.
R haut = e 1/ l1
+ e2/l2 = 0,01/2,50 +
0,05 / 1,15 = 4,75 10 -2 K W -1 m 2.
Rbas
= e3/l3
+ e4/l4 = 0,02/0,02 +
0,10 / 1,40 = 1,07 K W-1 m2.
Calculer
les flux de chaleur surfaciques circulant de part et d’autre du système
de chauffage.
Fhaut
=1/ Rhaut (Tc-Ts)
=(40-24) / (4,75 10-2) =3,37 102 W m-2.
Fbas =1/
Rbas
(Tc-Tf) =(40-7) / 1,07 =30,8 W m-2.
En
déduire la puissance totale délivrée par le système de chauffage par m²
de plancher chauffant.
Ftotal
= 3,37 10 2 + 30,8 = 3,68 10 2 W m-2.
Calculer
les températures T1 et T2.
Fhaut =(Tc-T1) l2 /e2 ; Tc-T1= Fhaut e2 / l2 ; T1=
Tc -Fhaut e2 /l2 .
T1=40-3,37 102
*0,05/1,15 = 25,3 °C.
Fbas
=(Tc-T2) l3
/e3 ; Tc-T2= Fbas e3 / l3 ; T2=
Tc -Fbas
e3 /l3 .
T2=40-30,8
*0,02/0,02 = 9,2 °C.
Calculer
le pourcentage de puissance perdue par le sol de fondation.
Fbas / Ftotal =30,8 /368=0,084
( 8,4 %).
Déterminer
l’énergie en joules puis en KWh apportée par m² de plancher par le
système de chauffage durant toute une journée.
Ftotal fois durée
(seconde) = 368*24*3600 =3,18 107 J m-2 ou 3,18 107
/(3,6 106) =8,8 kWh m-2.
|
|
|
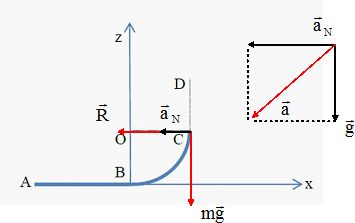
Le skateboardeur.
On s’intéresse à un skateboardeur effectuant un saut vertical sur un
tremplin assimilable à un quart de cercle de rayon r. Les phases du
mouvement sont les suivantes : phase d’accélération (de A à B), montée
du tremplin (de B à C), saut vertical (de C à D, avec D point de
hauteur maximale atteint par le skateboardeur), et retombée (de D à C
puis de C à B). On étudiera ici uniquement les phases de montée du
tremplin et de saut vertical dans lesquelles l’altitude du point B est
choisie comme référence pour l’énergie potentielle de pesanteur : Ep(B)
= 0 pour zB = 0. On assimilera le système {skateboardeur +
skateboard} à son centre d’inertie et on négligera les frottements.
Données : OB = r =1,5 m, vitesse du système à l’entrée du tremplin vB
= 25 km.h-1, masse du système m = 80 kg, intensité de la
pesanteur g = 9,81 m.s-2.
Quelle
est la vitesse du système au point C ?
Entre B et C, seul le poids travaille ; ( la rééaction du support,
perpendiculaire à la vitesse, ne travaille pas).
Théorème de l'énergie cinétique entre B et C : ½mv2C-½mv2B
= -mg OB ;
vC =( v2B
-2 gOB)½ avec vB = 25 /3,6 = 6,94 m/s.
vC
=( 6,942 -2 *9,81*1,5)½ =4,335 ~4,34
m/s.
Combien
vaut l’accélération normale du système au point C ?
aN = v2C/
r = 4,3352 / 1,5 = 12,53 ~12,5 m s-2.
Quelle
est la réaction du tremplin au point C ?
R = m aN = 80*12,53 = 1,0 103 N.
Combien
vaut l’accélération totale du système au point C ?
a =(a2N + g2) ½ = (12,532 + 9,812)
½ =15,9 m s-2.
A
quelle hauteur est situé le point D (à 0,1 prés) ?
Il s'agit d'un saut vertical ( chute libre ) avec vitesse initiale. Au
point le plus haut, la vitesse est nulle.
Appliquer à nouveau le théorème de l'énergie cinétique entre C et le
point le plus haut.
0-½mv2C
= -mg hmaxi ; hmaxi =v2C
/(2g) =4,3352 /(2*9,81) =0,96 m au dessus de C. (
~2,5 m au dessus de B).
|
.
|
|
L’écholocalisation
des chauves-souris.
Doc.1
Les cris - On classe les cris ultrasonores des chauves-souris en trois
groupes : les émissions de fréquence constante (FC), les émissions de
fréquence modulée décroissante (FM) et les émissions mixtes (FC-FM). En
général, ces ultrasons ne sont pas purs mais composés d’une fréquence
fondamentale et de plusieurs harmoniques Pour qu’une proie soit
détectable, elle doit avoir une dimension supérieure à la longueur
d’onde du signal ultrasonore.
Détection des distances - Pour estimer la distance à un objet (obstacle
fixe, proie…), les organes sensoriels de la chauve-souris enregistrent
le retard de l’écho par rapport à l’émission du signal.
Détection de la vitesse – La chauve-souris perçoit sa vitesse relative
par rapport à un objet grâce au décalage de fréquence du signal
réfléchi dû à l’effet Doppler. Les battements d’aile d’une proie
produisent un décalage des fréquences par effet Doppler oscillant qui
se superposent au décalage général engendré par les obstacles fixes
environnants. Chez certaines espèces, pour faciliter la détection de
ces oscillations, il existe un système de compensation : ces espèces
modifient la fréquence d’émission pour que la fréquence du signal
réfléchi par les obstacles fixes soit ramenée à une fréquence de
référence, celle qui est émise lorsque la chauve-souris est immobile,
et pour laquelle la sensibilité est maximale.
Donnée : Vitesse du son (ou des ultrasons) dans l’air : vson = 340 m.s-1.
Qu’appelle-t-on « cris ultrasonores » ?
Il s'agit d'un ensemble de sons brefs dont les fréquences sont supérieures à 20 kHz ( domaine des ultrasons).
Est-ce une onde longitudinale ou transversale ? Justifier.
Une onde ultrasonore est une onde mécanique longitudinale : la
direction de la perturbation ( variation de pression de l'air ) est la
même que la direction de propagation de l'onde.
À partir du Doc.2, déterminer la période T des signaux émis par les chauves-souris.
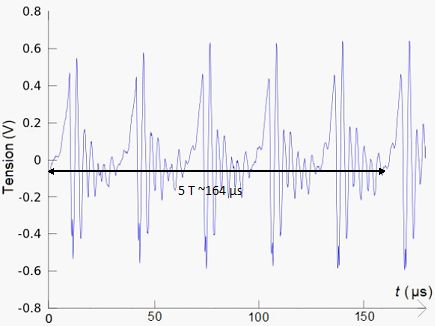
T= 164/5 ~33 µs = 3,3 10-5 s.
En déduire la fréquence fondamentale f des signaux émis par les chauves-souris. Conclure.
f = 1/T = 1/(3,3 10-5) ~30 kHz ; ces cris appartiennent bien au domaine des ultrasons.
Quelle est la fréquence de ses deux harmoniques les plus proches ?
Les fréquences des harmoniques sont des multiples de la fréquence du fondamental ; donc 60 kHz, 90 kHz ...
Nommer le phénomène qui perturbe la détection d’un écho pour que la proie soit détectable.
La diffraction de l'onde par une proie dont les dimensions sont de l'ordre de grandeur de la longueur d'onde des cris.
Calculer la dimension minimale d’une proie pour qu’elle soit détectable.
La taille de la proie doit être supérieure à 3 fois la longueur d'onde.
l = vson / f = 340 / (3,3 104) ~1,0 10-2 m ~1,0 cm ; taille minimale de la proie : 3 cm.
Réaliser
un schéma qui modélise la détection des distances d’une chauve-souris
qui se rapproche d’un obstacle fixe. Y faire apparaitre le parcours du
signal émis se rapprochant de l’obstacle, puis expliquer comment la
chauve-souris peut ainsi estimer les distances.
Le signal émis est réfléchi par l'obstacle puis détecté par la chauve souris. Connaissant la durée Dt de l'aller-retour et la célérité du son dans l'air, la distance d peut être calculée 2d = vson Dt.
En utilisant le Doc.3, calculer la distance séparant la chauve-souris du mur.
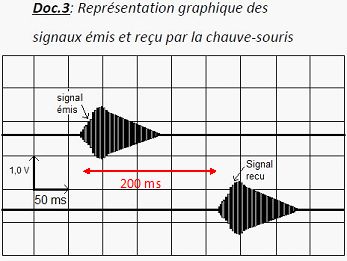
d = 340 * (100 10-3) =34 m.
Expliquer pourquoi « Les battements d’aile d’un insecte produisent un décalage des fréquences par effet Doppler oscillant ».
Les ailes de la proie se rapprochent, puis s’éloignent de la
chauve-souris, ce qui génère un décalage Doppler de la fréquence reçue
par la chauve-souris ; de plus, ce battement étant
périodique, ce décalage oscille entre deux valeurs extrèmes.
Donner un exemple d’utilisation de l’effet Doppler dans le domaine des ondes électromagnétiques.
Mesure de la vitesse des véhicules par les radars, détermination de la vitesse d'éloignement des galaxie en astrophysique.
Lorsque
la chauve-souris se rapproche d’un mur, l’écho perçu a-t-il une
fréquence plus grande, identique ou plus faible que celle du signal
émis ? Justifier simplement.
La fréquence de l'écho reçu est plus grande que celle du son émis.
La distance parcourue par l'onde réfléchie est plus faible ; la longueur d'onde diminue et f = vson / l. La fréquence va donc croître.
|
|
|
On propose deux relations pour l’expression de la fréquence perçue fR par une chauve-souris se dirigeant vers un mur à la vitesse de v = 20 km.h-1. On note f0 la fréquence du signal émis.
(1) : fR = (vson-v) f0 / (vson + v) ; (2) fR = (vson+v) f0 / (vson - v) ; (3) v = vson Df / (2f0).
Laquelle des relations (1) ou (2) est utilisable dans le cas décrit ? Justifier.
fR est supérieure à f0 : (2) convient, le numérateur doit être supérieur au dénominateur.
Calculer la fréquence fR de l’écho reçu lorsque le signal émis a pour fréquence 62 kHz.
v = 20 /3,6 = 5,56 m/s ; fR = (340+5,56) *62 / (340-5,56) ~64 kHz.
En
utilisant une des expressions précédentes, calculer la vitesse v d’une
proie par rapport à la chauve-souris, lorsque celle-ci perçoit un
décalage de fréquence Δf = 880 Hz pour un ultrason émis à la fréquence f0 = 93 kHz.
v = vson Df / (2f0) = 340*880 /(2*93 103) =1,6 m/s, vitesse relative par rapport à la chauve souris.
Combien de temps va mettre la chauve-souris pour rattraper sa proie, supposée située à 8,5 m d’elle en ligne droite ?
t = d/vproie) = 8,5 /1,6 = 5,3 s.
|
|
|