Interférences :
source monochromatique et polychromatique, : concours
audioprothésiste
Nancy 2013
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Source
monochromatique.
On réalise des interférences lumineuses à l’aide de fentes d’Young. Les
fentes F1 et F2 sont distantes de a = 0,20 mm et
les interférences sont observées sur un écran situé à la distance D =
1,0 m de ces fentes.
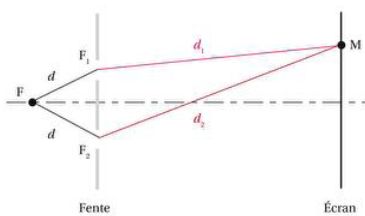
La source lumineuse F est monochromatique de longueur d’onde l = 0,64 μm et se comporte comme
une source synchrone et en phase. Elle est située à égale distance d de
F1 et F2.
Soit M un point de la figure d’interférences observée sur l’écran, M
est situé à la distance d1 de F1 et d2
de F2.
Les
ondes lumineuses issues de F1 et F2 sont-elles
cohérentes ?
Les sources F1 et F2 sont cohérentes, étant
obtenues à partir d'une source unique et un dispositif interférentiel (
dans ce cas deux fentes).
À
quelles conditions le point M sera-t-il sur une frange brillante ? sur
une frange sombre ?
Frange brillante : la différence de marche d = F2M-F1M
est un multiple entier de la longueur d'onde.
Frange sombre : la différence de marche d = F2M-F1M
est un multiple impair de la demi-longueur d'onde.
Que peut-on dire des
points M suivants :
M est tel que d2– d1= 0 : la différence de marche
est nulle, frange brillante.
M est tel que d2– d1= 3,20 μm = 5*0,64 = 5 l : frange brillante.
M est tel que d2– d1= 2,24 μm = 3,5 *0,64 =3,5 l = 7 l/2, frange sombre.
|
|
|
La source F n’est plus
monochromatique, mais des filtres permettent d’obtenir des radiations
monochromatiques différentes. Pour chaque radiation, on mesure la
longueur d’onde correspondant à 6 interfranges i (i est la distance
séparant le milieu de deux franges brillantes consécutives ou de deux
franges sombres consécutives).
|
.
|
|
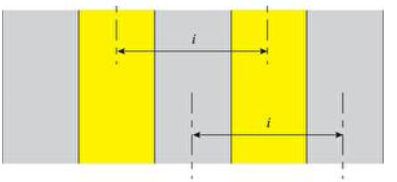
Pourquoi
mesure-t-on la distance correspondant à 6 interfranges plutôt que celle
mesurant 1 interfrange ?
On détermine l'interfrange avec une plus grande précision.
On a obtenu les résultats suivants. Compléter la seconde
ligne du tableau.
l(µm)
|
0,47
|
0,52
|
0,58
|
0,61
|
0,65
|
couleur
|
bleu
|
vert
|
jaune
|
orange
|
rouge
|
6
i (mm)
|
14,1
|
15,6
|
17,4
|
18,3
|
19,5
|
i
(mm)
|
2,35
|
2,6
|
2,9
|
3,05
|
3,25
|
|
|
Tracer la courbe
représentative de la fonction i=f (λ).
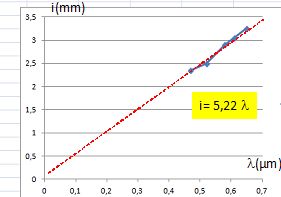
La
relation i =
lD/a
est-elle en accord avec la courbe obtenue précédemment ?
D/a = 1/(0,2 10-3 )=5,0 103.
Le coefficient directeur de la droite est égal à 5,22 mmm µ-1
soit 5,22 103.
Ecart relatif entre les deux valeurs ( 5,2-5) / 5 = 0,04 ( 4 %). les
deux valeurs sont cohérentes.
Comment
faudrait-il modifier le dispositif expérimental pour obtenir des
mesures avec une plus grande précision ?
On peut doubler ou tripler la distance D et utiliser une lumière rouge
de plus grande longueur d'onde.
Quelle
serait la valeur de l’interfrange obtenu avec une radiation de longueur
d’onde 0,50 μm ?
i = l D/a = 0,50 10-6 *1/(0,2 10-3) =2,5 10-3
m = 2,5 mm.
On dispose d’une source monochromatique de longueur d’onde inconnue.
Comment
feriez-vous expérimentalement pour la déterminer ?
On réalise à l'aide du dispositif précédent des interférences et on
détermine l'interfrange. La longueur d'onde peut être déterminée en
utilisant le graphe précédent.
|
| |
|