Glissade sur un
plan, chute libre, concours ergothérapeute 2012.
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Un
solide ponctuel glisse sur un plan incliné ( a = 30° ). On donne g = 10 m s-2
; v0 = 1,0 m/s et H= OA =2,0 m.
A la date t=0, le mobile passe en A.
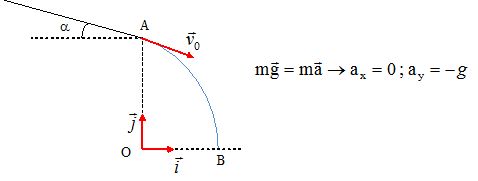
Quelles sont les conditions initiales ?
Coordonnées du point A dans le repère indiqué sur le schéma : xA =0 ; yA =2.
Dans ce repère coordonnées de la vitesse initiale :
v0x =v0 cos a = cos 30 =0,866 ; v0y = -v0 sin a = -sin 30 = -0,5.
Etablir les équations horaires du mouvement et montrer que le mouvement est plan.
Le mobile est en chute libre ( il n'est soumis qu'à son poids ).
Le poids et le vecteur vitesse initial étant dans un plan vertical, le mouvement s'effectue dans ce plan.
Ecrire la seconde loi de Newton dans le repère proposé.
La vitesse est une primitive de l'accélération :
vx =ax t +v0x = 0 +v0 cos a =0,866 m/s.
vy =ay t +v0y = -gt -v0 sin a = -10t -0,5.
La position est une primitive de la vitesse :
x =v0 cos a t +xA =v0 cos a t =0,866 t. (1)
y = -½gt2 -v0 sin a t +yA.
y = -5t2-0,5t+2. (2)
Montrer que la trajectoire est parabolique entre A et B.
(1) donne t = x/0,866. Repport dans (2) :
y = -5(x/0,866)2-0,5(x/0,866) +2.
y = -6,67 x2-0,577 x +2.
Il s'agit de l'équation d'une branche de parabole.
|
|
|
Déterminer les coordonnées de B, la vitesse en B et la durée du trajet AB.
yB=0 ; -6,67 x2-0,577 x +2 =0.
Résoudre : D =0,5772+4*2*6,67 =53,67 ; D½ =7,326.
On conservera la racine positive : xB =(0,577-7,326) / (-2*6,67) =0,506 ~0,51 m.
xB =0,866 t ; t = 0,506/0,866 =0,584 ~0,58 s.
vx =0,866 ; vy =-10t-0,5 = -10*0,584-0,5 = -6,34.
vB = (0,8662 +(-6,34)2)½ ~6,4 m/s.
Autre méthode : appliquer le théorème de l'énergie cinétique entre A et B.
½mvB2-½mvA2 = mgH ; vB2-vA2 = 2gH.
vB2=vA2 +2gH = 1+2*10*2 = 41 ; vB =6,4 m/s.
|
.
|