Particule alpha dans un champ électrostatique. Concours kiné Berck 2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . . . A la date t=0 un faisceau homocinétique de particules alpha pénètre en un point O d'un condensateur plan. O est situé à égale distance des deux plaques parallèles et horizontales du condensateur plan. Chaque particule est animée d'une vitesse horizontale v0. On place à la distance L de la sortie du condensateur plan un écran vertical luminescent sur lequel les impacts des particules alpha créent des taches lumineuses. En l'abscence de champ électrostatique, il se forme une tache en O' de l'écran. On créé un champ électrostatique uniforme E en appliquant une tension UAB entre les deux plaques A et B du condensateur. Les particules sont déviée vers le haut et il se forme une tache au point P de l'écran. On négligera le poids de la particule  et cette expérience est réalisée dans le vide. 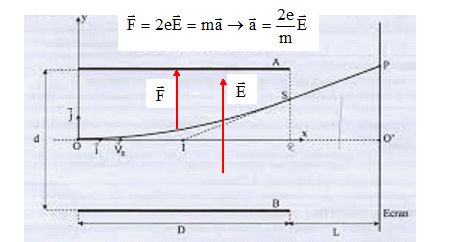Une particule alpha est un noyau d'hélium 42He. e = 1,60 10-19 C ; masse d'une particule alpha m = 6,64 10-27 kg. O'P =24,3 mm ; |UAB|=1,5 102 V ; D = 14,0 cm ; L = 20,0 cm ; d = 5,00 cm. La tangente à la trajectoire en S passe par le point I ( ½D ; 0). La valeur du champ électrostatique d'un condensateur plan est E =|UAB| /d. Préciser le signe de la tension UAB. Les particule alpha chargées positivement sont déviées vers le haut. La plaque A est donc négative et en conséquence UAB= VA-VB est négative. Décrire le mouvement de la particule entre S et P. Le champ électrostatique est nul entre S et P : la particule n'est donc soumise à aucune force. D'après le principe d'inertie, le mouvement de cette particule est rectiligne uniforme, sa vitesse en S n'étant pas nulle. Déterminer l'ordonnée yS. O'P / yS =(L+½D) / (½D) ; yS = ½O'P D / (L+½D). yS =0,5*2,43*14,0 /(20,0 +7,00) =0,63 cm. Etablir l'expression de la trajectoire de la particule dans le condensateur plan. Accélération ( 0 ; 2e/m E) ; vitesse initiale : (v0 ; 0). La vitesse est une primitive de l'accélération : v0 ;  2e/m E t. La position initiale coïncide avec l'origine O du repère. Position : x = v0 t ; y = ½2e/m E t2 =e/m E t2 . Au point S : x = D= v0 tS soit tS = D/v0. Repport dans y : yS = e/m E(D/v0)2. t = x/v0 ; y =e/m E (x/v0)2 . Calculer v0. E =|UAB| /d = 150 / 0,0500 = 3,0 103 V /m. v02 = eED2/(myS) ; v0 =D(eE/(myS))½ =0,14(1,6 10-19* 3,0 103 /(6,64 10-27*6,3 10-3))½=4,74 105 m/s. . On modifie la valeur de la tension UAB, la valeur de v0 restant inchangée. Déterminer la valeur maximale de cette tension à partir de laquelle la particule ne peut plus sortir du condensateur. Dans ces conditions yS est égale à ½d = 2,5 cm. Or yS = e/m E(D/v0)2 et E = |UAB| /d. ½d =e/m |UAB|max /d (D/v0)2  ; |UAB|max = md2v02/(2eD2)=6,64 10-27*0,052*(4,74 105)2/(2*1,6 10-19*0,142)=595 V.

menu