Chute libre, travail, énergie. Concours audioprothésiste Bordeaux 2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Dans le champ de pesanteur uniforme g, une boule en fer de masse m = 700 g est lancée vers le haut à t=0, depuis le niveau z0 = + 1 m, avec une vitesse initiale v0 = -4 m/s. On néglige les frottement et on note P le poids de la boule. On étudie le mouvement vertical de la boule. 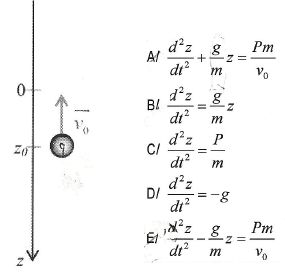l'équation différentielle du mouvement est : Il s'agit d'un mouvement de chute libre verticale avec une vitesse initiale. La deuxième loi de Newton écrite sur l'axe vertical descendant s'écrit : m d2z/dt2= P = mg soit d2z/dt2=g= P/m. C est exact. La loi horaire décrivant la position de la boule au cours du temps est : z(t) = -½gt2 +v0t+z0 ; z(t) = ½gt2 -v0t-z0 ; z(t) = -½gt2 +v0t ; z(t) = ½gt2 +v0t+z0 ; z(t) = ½gt2 -v0t. La vitesse est une primitive de l'accélération : v(t) = dz/dt = gt +constante.  A t=0, v(0) =v0 ; v(t) = gt +v0. La position est une primitive de la vitesse : z(t) = ½gt2 +v0t + constante ; à t = 0 z(0) = z0. Soit tmax la date à laquelle la boule atteint sa hauteur maximale. La vitesse de la boule vaut à cet instant :  0 ; -1 m/s ; -6 m/s ; 2 m/s ; 6 m/s. à tmax la composante verticale de la vitesse est nulle. L'expression de tmax est alors :. -v0/g ; (2v0 /(g-v0z0))½ ; (2v0 /(g-v0z0))½ -z02/g ; (2v0 /(g-v0z0))½ +z02/g ; v0/g. v(tmax) = gtmax +v0 = 0 ; tmax = -v0 /g. L'expression de la hauteur maximale zmax atteinte par la boule est : ½v02/g+z0 ; ½v02/g-z0 ; -½v02/g-z0 ; -½v02/g+z0 ; ½v02z0 /g. zmax = ½gtmax2 +v0tmax +z0 = ½g(-v0 /g)2 +v0(-v0 /g) +z0 ; zmax =-½v02/g+z0. Un oscillateur est constitué d'un dispositif solide-ressort. La période propre de l'oscillateur est : (k/m)½ ; (m/k)½ ; 2p(k/m)½ ; 2p(m/k)½ ;1/(2p) (k/m)½. Une masse de 1000 kg est suspendue au bout d'un ressort vertical. Sachant que l'on veut obtenir des oscillations de période propre égale à 1 s, la raideur du ressort est environ : 50 N/m ; 1300 N/m ; 7 kN/m ; 1kN/m ; 40 kN/m. 1 = 2*3,14(1000/k)½ ; 1 ~4*10*1000/k = 40 000/k ; k~40 000 = 40 kN/m. Une bille de masse m =50 g peut glisser dans un bol de forme hémisphérique de rayon intérieur R= 10 cm. Elle est alors soumise à une force de frottements que l'on supposera constante, de valeur F = 10 mN. A l'instant initial, la bille est lâchée sans vitesse initiale depuis un point A tel que l'angle que fait la direction (OA) avec la verticale (OB) est un angle droit. 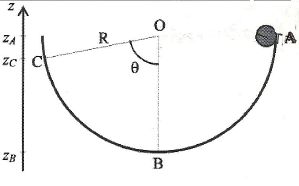Quel est le travail du poids sur le trajet de A à B ? ( -60 mJ ; +60 mJ ; +50 mJ ; +120 mJ ; -50 mJ ) Le travail du poids est moteur en descente et vaut m g R = 50*10*0,10 = 50 mJ. Quel est le travail de la force de frottement au cours du trajet AB ? ( -150 mJ ; -1,5 mJ ; -30 mJ ; +1,5 mJ ; +150 mJ ) Le travail des frottements est résistant et vaut -F arc(AB)= -F ½p R = 10*0,5*3,14*0,10 ~-1,5 mJ. On suppose que l'énergie potentielle  de la bille est nulle au point B. L'énergie mécanique en A est : (( 1,5 mJ ; 30 mJ ; 50 mJ ; 80 mJ ; 48,5 mJ ). L'énergie mécanique est la somme de l'énergie cinétique et de l'énergie potentielle. En A la vitesse ( donc l'énergie cinétique ) est nulle. EM(A) = mgR = 50 mJ. L'énergie cinétique de la bille en B est : 1,5 mJ ; 48,5 mJ ; 50 mJ ; 51,5 mJ ; 0 mJ. L'énergie mécanique diminue du travail des frottements : EM(B) = EM(A) - |WF |=50-1,5 = 48,5 mJ. L'énergie potentielle est nulle en B ; EM(B) = Ec B = 48,5 mJ. La vitesse de la bille au passage en B est : 0,24 m/s ; 1,39 m/s ; 1,41 m/s ; 1,44 m/s ; 0 m/s. v = (2 Ec B / m)½ = (2 *48,5 / 50)½ =1,39 m/s. Un des murs d'une maison a une superficie S. Comme il est en contact avec le milieu extérieur, il est d'abord constitué d'une épaisseur "e" de béton de conductivité l. En réfléchissant à l'influence physique de chacun des paramètres, retrouvez l'expression dela résistance thermique Rth du mur : (Sl/e ; l/(Se) ; Sel ; Se/l ; e/(Sl). Flux thermique F = DT/ Rth. Ce flux est d'autant plus faible que Rth est grand ; Rth est d'autant plus grand que e est grand et l est faible. L'unité de résistance thermique est : kelvin par watt ; watt par kelxvin par mètre carré ; watt par degré Celsius ; kelvin par watt par mètre carré ; watt par kelvin. Rth =DT/ F ; RTh s'exprime en  K W-1. L'unité de la conductivité thermique est :  W m2 K-1 ; W m-2 K-1 ; W K m-1 ; W m-1 K-1 ; W m K-1. Rth = e/(Sl) ; l = e/(S Rth)  ; l s'exprime en W m-1 K-1.

menu