Métallurgie de l'uranium Concours ingénieur de l'industrie et des Mines 2013

   Métallurgie de l'uranium
Concours ingénieur de l'industrie et des Mines 2013

En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.

. .

Propriétés de l'uranium.
L'uranium est un élément qui possède plusieurs isotopes.
Définir isotopes. Citer deux isotopes d'un autre élément. Dire pourquoi, d'un point de vue purement chimique, il n'y a pas de différence de comportement entre 2 isotopes .
Deux isotopes ne se différencient que par leur nombre de neutrons. Ils ont le même numéro atomique Z.
Exemple : ³⁵₁₇Cl et ³⁷₁₇Cl ; ¹²₆C et ¹⁴₆C.
La seule différence de comportement est liée à leur différence de masse : ils ont donc les mêmes propriétés chimiques.
Donner la composition de chacun des noyaux de l'uranium.
²³⁵₉₂U : 92 protons et 235-92 =143 neutrons ; ²³⁸₉₂U : 92 protons et 238-92 =146 neutrons.
La masse molaire de l'uranium naturelle est 238,0289 g/mol. Masse molaire de l'uranium 235 : 235,0439 g/mol ; de l'uranium 238 : 238,0508 g/mol.
En déduire la teneur en uranium 235.
On note x la teneur en uranium 235 de l'uranium naturel :
235,0439 x +238,0508(1-x) = 238,0289 ; 3,0069 x =0,0219 ; x = 0,0073 (0,73 %).
L'uranium naturel existe sous trois formes cristallines notées a, ß et g. La variété g est stable entre 775°C et 1130°C et cristallise sous forme cubique centrée.
Représenter cette maille. Combien la maille contient-elle d'atomes ?

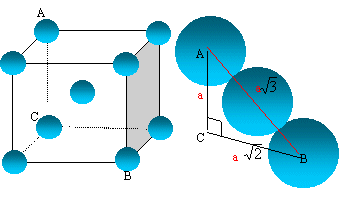
La tangence s'effectue suivant la grande diagonale du cube :
a racine carrée (3) = 4 R
Les 8 atomes situés aux sommets du cube sont communs à 8 mailles et comptent pour 1/8=0,125.
celui du centre, commun à une seule maille, compte pour une unité.
nombre d'atomes d'uranium appartenant à la maille : 8* 0,125 +1 = 2.
Le paramètre de maille est 350 pm.
En déduire le rayon moyen de l'uranium dans cette structure supposée compacte.
R = 350*3^½/4 =152 pm.

.
.

Elaboration du combustible.
Réduction de UO₃ :
3UO₃(s) + 2NH₃(g) = 3UO₂(s) +N₂(g) +3H₂O(g) (1).
Calculer D_rH°(298K).
D_rH° =3D_fH°(UO₂(s))+3D_fH°(H₂O(g))-2D_fH°(NH₃(g))-3D_fH°(UO₃(s)).
D_rH° =3*(-1085)+3(-241,8)-2(-46,19)-3(-1224)= -216 kJ/mol.
Pour favoriser la formation de UO₂(s), a-t-on intérêt à travailler à haute ou à basse température ? A-t-on intérêt à travailler à pression élevée ? Justifier.
D_rH° est négatif : la réaction est exothermique et sera favorisée par un température peu élevée.
Initialement il y a 2 moles de gaz, finalement il y a 4 moles de gaz : la réaction est favorisée par une pression assez faible.
Calculer D_rS°(298K) en se plaçant dans l'approximation d'Ellingham), qu'on rappellera, déterminer D_rG°(298K).
L'enthalpie standard  de réaction et l'entropie standard D_rS° de la réaction ne dépendent pas de la température en dehors de tout changement de phase.
D_rS° =3S°(UO₂(s))+3S°(H₂O(g))+S°(N₂(g))-2S°(NH₃(g))-3S°(UO₃(s)).
D_rS° =3*77,8 +3*188,7+191,5-2*192,3-3*98,6=310,6 J K^-1 mol^-1.
D_rG° =D_rH°-TD_rS° =-2,16 10⁵ -298*310,6 =-3,09 10⁵ J/mol.
On travaille à 900 K sous 1 bar. Calculer la constante d'équilibre et conclure.
D_rG° =-RT ln K ; ln K = D_rG° /(-RT) =3,09 10⁵ /(8,314*900) =41,3 ; K = 8,6 10¹⁷.
La constante K étant grande, la réaction est totale.

.

Fluoration de UO₂.
UO₂(s) +4HF(g) = UF₄(s) +2H₂O(g) (2).
D_rG°(T) =-235,2 +0,2435 T en kJ/mol.
On maintient la température à 700 K et la pression à 1 bar.
Déterminer la constante d'équilibre K₂ à 700 K.
D_rG°(700) =-235,2+0,2435 *700 = -64,75 kJ/mol = -6,475 10⁴ J/mol.
ln K₂ = D_rG° /(-RT) =6,475 10⁴ /(8,314*700) =11,13 ; K₂ = 6,79 10⁴.
On part de 1 mole de UO₂ et 1 mole de HF.
Quelle est la composition finale ?

avancement (mol)
UO₂(s) +4HF(g) = UF₄(s) +2H₂O(g)

initial
0
1
1
0
0

à l'équilibre
x
1-x
1-4x
x
2x

0,243
0,757
0,028
0,243
0,486

Nombre total de mol à l'équilibre : n =2-2x ; pression partielle de HF : p₁=(1-4x) / ((2-2x) ; pression partielle de H₂O : p₂=2x/(2-2x) = x/(1-x).
K₂ = p₂² / p₁⁴ =16x²(1-x)² / (1-4x)⁴ ; K₂ (1-4x)⁴ =16x²(1-x)² ; K₂^½ (1-4x)² =4x(1-x) ; K₂^½ =260,6.
260,6(1+16x²-8x) =4x-4x² ; 4,173 10³ x² -2,0886 10³ x+260,6=0 ;
x² -0,500 x +0,06245=0 ; D = 0,5² -4*0,06245 =2 10^-4 ; x = ½(0,5-1,414 10^-2) =0,243.
Même question en partant de 0,1 mole de UO₂ et 1 mole de HF. Que remarque-t-on dans ce cas ?

avancement (mol)
UO₂(s) +4HF(g) = UF₄(s) +2H₂O(g)

initial
0
0,1
1
0
0

à l'équilibre
x
0,1-x
1-4x
x
2x

0,1
0
0,6
0,1
0,2

UO₂(s) est en défaut et la réaction est totale : à l'équilibre x = 0,1 mol. Le rendement par rapport au réactif en défaut est de 100 %.

Obtention de l'uranium métallique.
UF₄(s) + 2Mg(s) =U(s) + 2MgF₂(s) (3).
Calculer D_rH°(298K).
D_rH° =2D_fH°(MgF₂(s))-D_fH°(UF₄(s)).
D_rH° =2*(-1124)-(-1921)= -327 kJ/mol.
D_rH° est négatif, la réaction est exothermique.
Quelles conditions doivent être réunies pour obtenir les produits sous la température la plus élevée possible ?
La réaction (3) est favorisée par des températures peu élevées. Les réactifs seront utilisés en proportions stoechiomètriques.
Pour un système adiabatique, l'énergie libérée par la réaction est entièrement gagnée par les produits.
A partir de la température initiale 298 K, calculer la température maximale atteinte. On fait l'hypothèse qu'il n'y a pas de changement d'état.
Les réactifs étant en proportions stoechiométriques et la réaction étant totale, les réactifs disparaissent rapidement. le milieu réactionnel ne contient que les produits.
|D_rH°| =(C_p(U(s))+2C_p(MgF₂(s))) ( T_f-T_i) ;
3,27 10⁵ =(27,67 +2*61,5)(T_f-298) =150,67 T_f-4,49 10⁴ ; T_f= 2468 K.
L'hypothèse formulée est inexacte, les température de fusion des produits étant bien inférieures à 2468 K.
La température réelle est moins grande mais l'uranium reste tout de même à l'état liquide. Expliquer en quoi c'est un avantage.
Le métal à l'état liquide peut être récupéré par coulée.



menu