Fission de
l'uranium 235, déchets radioactifs :
Concours technicien supérieur de l'industrie et des Mines 2010
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
Energie et
puissance produite.
Une centrale nucléaire constituée de 4 tranches a une production
annuelle d'énergie électrique E = 2,60 1013 Wh ( soit 6,5 %
de la production nationale ).
Déterminer
la puissance moyenne P délivrée par la centrale puis calculer la
puissance électrique moyenne Pe fournie par l'une des tranches.
P (W)= énergie ( Wh) / durée ( heure) = 2,60
1013 /
(365*24) = 2,97
109 W =
2,97
103 MW
Pe
= 0,25 P =0,25* 2,97
103 =
7,4 102 MW.
Calculer
la consommation d'énergie électrique nationale ET en joules.
E =
2,60 1013 *3600 =9,36 1016 J
ET =E / 0,065 =9,36
1016 /0,065 =1,44 1018 J.
Source d'énergie
:
L'uranium naturel est un mélange de deux isotopes 23892U
( 99,3 %) et 23592U ( 0,7 %).
Seul l'isotope 23592U
est fissible. Sous l'impact de neutrons lents, il peut se produire la
réaction représentée par l'équation suivante :
23592U
+ 10n
---> 139xXe
+ 9538Sr
+ y10n. (1)
Masses des noyaux ( en u ) participants à la réaction :
m(139xXe) =
138,8882 u ; m(9538Sr)
=94,8946 u ; m(23592U)
=235,0134 u ; m(10n)
=1,0087 u ; m(11p)
=1,0073 u ;
1 u = 1,66 10-27 kg ; 1 MeV = 1,6 10-13 J.
Calculer
l'énergie de liaison El en MeV puis
l'énergie moyenne de liaison par nucléon du noyau d'uranium 235.
Le noyau 23592U
possède 92 protons et 235-92 = 143 neutrons.
El =[92 m(11p)
+143m(10n)-m(23592U)]c2.
El
=[92 *1,0073 +143*1,0087-235,0134]*1,67
10-27 *(3 108)2 =2,84 10-10
J
ou 2,84
10-10 /(1,6 10-13) =1,776 103 MeV
~1,78 103 MeV.
El
/A = 1,776
103 /
235 = 7,56 MeV/nucléons.
Justifier à partir
de la courbe d'Aston, l'intérêt énergétique de cette réaction.
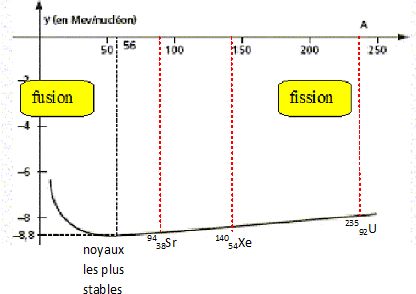
Les noyaux fils sont plus stables que le noyau père : cette réaction
libère donc de l'énergie.
|
| .
. |
|
|
Enoncer les lois de
conservation relatives aux transformations nucléaires et en
déduire les entiers x et y.
Conservation de la charge : 92 = x +38 d'où x =54.
Conservation du nombre de nucléons : 235 +1 = 139+95+y d'où y = 2.
Les neutrons lents dans le coeur du réacteur ont une vitesse v = 64
km/s.
Calculer
leur énergie cinétique Ec en J et en eV.
Ec = ½mv2 avec m = 1,0087 *1,66 10-27
= 1,6744 10-27 kg et v = 6,4 104 m/s.
Ec
=0,5* 1,6744 10-27*(6,4
104 )2 =3,43 10-18
J ou 3,43
10-18 /(1,6 10-19) =21,4 eV.
|
.
|
|
Calculer la perte de masse Dm, exprimée en u, au cours de la fission d'un noyau d'uranium.
Dm =
m(139xXe) +m(9538Sr) +m(10n) -m(23592U) =138,8882 + 94,8946 + 1,0087 - 235,0134= -0,2219 u
Calculer en J puis en MeV, l'énergie E1 libérée par la fission d'un noyau d'uranium 235.
E1 = Dm c2 = -0,2219 *1,66 10-27 *(3 108)2 = -3,32 10-11 J ou -3,32 10-11 /(1,6 10-13) = -207 MeV.
Le signe moins traduit le fait que le système libère de l'énergie dans le milieu extérieur.
Estimer
en J puis en TEP, l'énergie libérée par la fission d'une tonne
d'uranium naturel si toutes les réactions de fission libèrent l'énergie
calculée précédemment.
M(23592U) =235 g/mol ; NA = 6,02 1023 mol-1 ; 1 TEP = 42 GJ.
1000 kg d'uranium naturel contiennent 7 kg d'uranium 235.
Quantité de matière d'uranium 235 : 7000 / 235 = 29,79 mol.
Nombre de noyaux d'uranium 235 = nombre de fission = 29,79 * 6,02 1023 =1,79 1025.
Energie libérée : 3,32 10-11 *1,79 1025 = 5,95 1014 J = 5,95 106 GJ ou 5,95 106 /42 =1,4 104 TEP.
L'isotope 23892U non fissile est dit fertile. Il peut capter un neutron rapide suivant l'équation :
23892U +10n ---> 23992U.
23992U est radioactif ; il se transforme en neptunium 23993Np. Ce dernier, également radioactif, se transforme en plutinium 23994Pu fissile.
23992U ---> 23993Np + 0-1e ( ß-).
3993Np ---> 23994Pu + 0-1e ( ß-).
Le combustible des surrégénérateurs est un couple fissile fertile 23994Pu et 23892U.
Quel intérêt présente l'usage d'un tel combustible ?
La fission du plutonium libère des neutrons, susceptibles de rendre
fissile l'uranium 238. On utilise ainsi au mieux l'uranium naturel.
|
Déchets radioactifs.
Dans le combustible irradié d'un réacteur nucléaire, on trouve du
zirconium 95 de demi-vie radioactive 64 jours et du plutonium 241 de
demi-vie radioactive14,3 ans. On immerge le container dans la piscine
de la Hague pendant 3 ans.
|
|