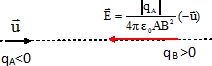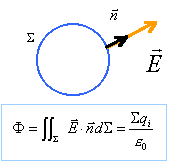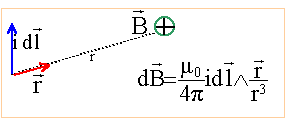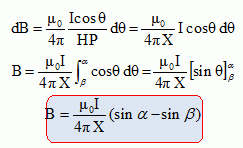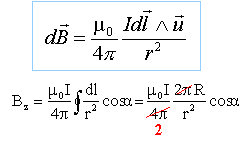Electrostatique, électromagnétisme. Concours itpe 2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Etude de deux charges dans le vide. On considère deux charges ponctuelles qA et qB placées dans le vide à la distance r=AB. Définir la loi de Coulomb et l'expression de la force électrostatique entre les deux charges. Deux corps A et B de charges respectives qA et qB séparés d'une distance d exercent l'un sur l'autre des forces opposées attractives ou répulsives, importantes dans l'infiniment petit, négligeables dans l'infiniment grand.   Donner l'expression du champ électrique créé par la charge qA. 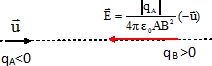Etude d'une distribution de charges. On considère une distribution de charges ponctuelles ( q1, q2...qi...) notée D, de charge totale Q. Définir le théorème de Gauss appliqué à ces charges. le flux du champ électrique à travers une surface S fermée est égal à la somme des charges contenues dans le volume V délimité par cette surface divisée par e0. On considère une sphère uniformément chargée en surface de densité surfacique positive s de charge totale Q. D'après la symétrie sphérique de la distribution de charge, le champ en un point M quelconque est radial. Déterminer l'expression du champ électrique en un point M. Soit un point M situé à l'intérieur de la sphère, à une distance OM=x du centre. Par raison de symétrie le champ est radial. 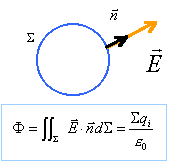On considère une sphère S , de centre O et de rayon x. D'après le théorème de Gauss, le flux du vecteur champ électrique à travers la surface S est nul car il n'y a pas de charge à l'intérieur de S. si x < R, le champ électrique est nul à l'intérieur de la sphère.  Soit un point M situé à une distance x > R : F = E 4px² D'autre part la charge contenue à l'intérieure de S est la charge totale de la sphère de rayon R : Q = s 4pR². d'où E = s R² / (e0x²) On retrouve la discontinuité de la composante normale du champ (s / e0) à la traversée d'une surface chargée. En déduire l'expression du potentiel ( le potentiel électrique est nul à l'infini).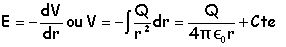 La constante d'intégration est nulle, le potentiel électrique étant nul à l'infini. A l'extérieur de la sphère : V = Q/(4p e0 r). A la surface de la sphère : V = Q/(4p e0 R). Il y a continuité du potentiel à la traversée de la surface de la sphère. Potentiel constant à l'intérieur de la sphère V0 = Q/(4p e0 R). 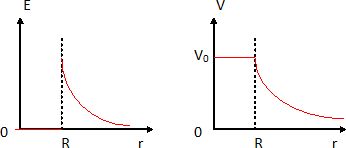Représenter l'allure du champ électrique et du potentiel en fonction de r.   . . Le champ magnétostatique. Enoncer la loi de Biot et savart pour un élément de courant Idl. 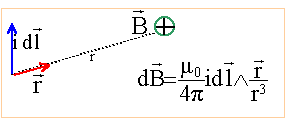Que peut-on dire de la continuité du champ B pour une distribution volumique de courants ? Le champ B est continu.   Que peut-on dire de la continuité du champ B à la traversée de la surface d'une distribution surfacique de courants ? La composante normale du champ magnétique se conserve ; la composante tangentielle du champ magnétique subit une discontinuité. Champ d'un fil rectiligne. Exprimer le chgamp magnétique créé par ce fil en un point M.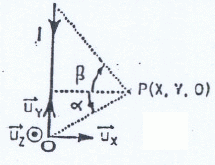 L'élément de courant Idl crée en P un champ magnétique  élémentaire dB, perpendiculaire au plan formé par Idl et MP, orienté vers l'avant du plan. 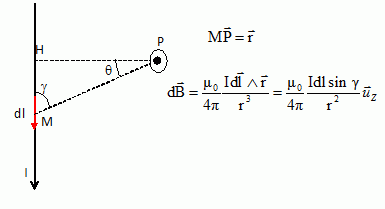tan q = MH /HP  ; MH = HP tan q  ; dériver dMH = dl = HP dq / cos2q. De plus : sin g = cos q, et r = HP / cos q, d'où : dl sin g / r2 = HP cos q dq . 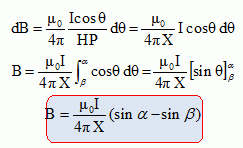Le champ B est-il défini sur le fil ? Justifier. Non, la distance HP= X est alors nulle, ce sui conduit à une division par zéro. Même question si le fil est infiniment long. Les angles a et b sont orientés dans le sens du courant : a est positif et b est négatif. a tend vers ½p et b tend vers -½p, d'où : B = µ0I / ( 2 p X). . Champ d'une bobine circulaire plate. Considérons une spire circulaire plate. Déterminer l'expression du champ au centre de la spire et en un point de son axe. 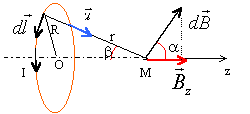Tout plan passant par Oz est un plan d'antisymétrie du système. En conséquence le champ magnétique est porté par l'axe Oz. 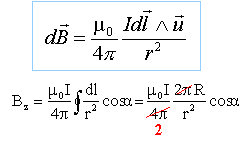On applique la relation de Biot et Savart : avec cos a = sin b, angles complémentaires. r = R / sin b  ; cos a =R / r = R /(R2+z2)½. On pose B0 =µ0I / (2R) ; Bz = B0[ R2/(R2+z2)]3/2. B0 représente le champ magnétique créé au centre O de la spire. On remplace maintenant la spire par une bobine plate de même rayon R, constituée de N spires. B0 =Nµ0I / (2R). Champ créé par un solénoïde. Le solénoïde est constitué de N spires circulaires jointives. 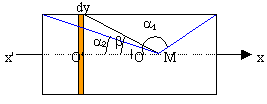O est l'origine de l'axe. On pose O'M=y. La tranche de solénoïde de rayon R, d'épaisseur dy compte n1dy spires (n1 : nombre de spires par mètre). Le champ dB crée par cette tranche est : dB = m0I/(2R) sin3(b) n1dy exprimons dy en fonction de db y= R cotan(b) dy=Rdb /sin²(b) d'où sin²(b)dy = Rdb dB = m0I/2 sin(b) n1db=m0I/2 n1d(-cos(b)) intégrer entre les angles a1 et a2. B=m0I/2 n1(cos(a2)-cos(a1)) solénoïde infiniment long a2=0 et a1=p B=m0 n1I. Le champ magnétique est uniforme.

menu