Mesure de la masse d'Uranus. Concours itpe 2014 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Le satellite Titania est en orbite autour d'Uranus à une altitude de 4,11 105 km et sa période de révolution est de 8,71 jours. On suppose que le satellite de centre C est un solide ponctuel et que le déplacement se fait sans frottement. On note m la masse du satellite et M la masse d'Uranus. Rayon d'Uranus R = 2,53 104 km. Etude cinématique du satellite. On suppose que le mouvement du satellite est circulaire de rayon r = R+h. Dans quel référentiel est décrite l'orbite de Titania ? Référentiel Saturnocentrique. Déterminer l'expression de la vitesse de Titania autour de la planète Uranus. 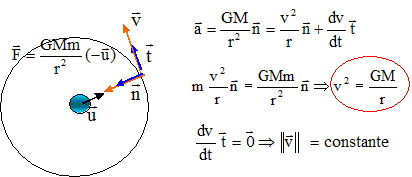Montrer que le vecteur accélération a pour expression :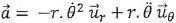 . . 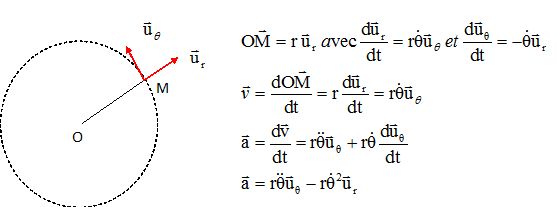Etude dynamique du satellite. Donner l'expression de la force gravitationnelle exercée par Uranus sur le satellite. En déduire l'expression de l'accélération. 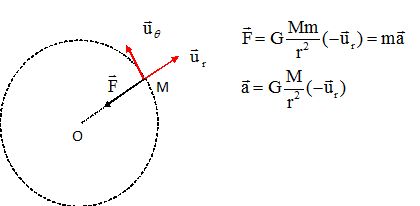En utilisant l'expression de l'accélération dans la base de Frenet, montrer que le moyuvement du satellite est uniforme et en déduire l'expression de la vitesse. 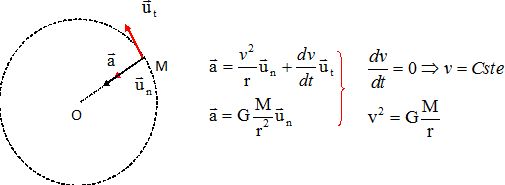  . Déterminer l'expression de la vitesse v du centre d'inertie de Titania en fonction de R, h et T. Le satellite décrit la circonférence 2p(R+h) à la vitesse constante v en T seconde. v = 2p(R+h) /T. Exprimer puis calculer la masse d'Uranus. v2 = 4p2(R+h)2 /T2 = GM/(R+h) ; M =4p2(R+h)2 /(T2 G). M = 4*3,142(2,53 107+4,11 108 )3 /((8,71*24*3600)2*6,63 10-11)=8,72 1025 kg. Loi de Kepler et mesure de la masse d'Uranus. L'observation d'Obéron, le deuxième satellite d'Uranus, peut également nous permettre de déterminer la masse d'Uranus à partir des lois de Kepler. On considère les aires balayées par le segment joignant Uranus à Titania pendant une même durée en différents points de l'orbite. Elles correspondent aux aires des surfaces formées par les points N P1 P2 autour du péricentre P d'une part et N A1 A2 autour de l'apocentre d'autre part. 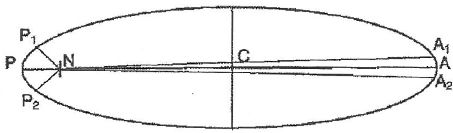On donne le demi-grand axes du satellite Oberon : a = 5,84 105 km et la période de révolution d'Oberon T = 323 heures. Enoncer la première loi de Kepler.  Dans le référentiel Saturnocentrique, l'orbite de chaque satellite de Saturne est une ellipse dont l'un des foyers est le centre de Saturne. Enoncer la seconde loi de Kepler.  Le mouvement de chaque satellite est tel que le segment de droite reliant Saturne et le satellite balaie des aires égales pendant des durées égales. Comparer les vitesses de Titania aux points A et P. La distance A1A2 est inférieure à la distance P1P2. Ces distances sont parcourues pendant la même durée T. La vitesse en A est donc inférieure à la vitesse du satellite en P. Enoncer la troisième loi de Kepler. Le carré de la période est proportionnel au cube du rayon de l'orbite. On définit la vitesse aréolaire par dA/dt = Cste = ½C. Montrer que (pab)2/T2 = C2/4. ( a est le demi-grand axe et b le demi-petit axe ). L'ellipse d'aire A = pab est décrite en T seconde. A/T = pab / T = ½C. Sachant que le paramètre p ~ C2/(GM) =b2/a, montrer que : T2/a3~ 4p2/(GM). p2a2b2/T2 = C2/4 ; p2a2aC2/(GMT2 )= C2/4 ; p2a3/(GMT2 )= 1/4 ; T2/a3~ 4p2/(GM). Exprimer puis calculer la masse d'Uranus. M = 4p2a3/(GT2)= 4*3,142*(5,84 108)3 / (6,63 10-11*(323*3600)2)=8,77 1025 kg.

menu