Le télescope de
Newton.
Concours itpe 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
Le télescope de Newton est constitué de trois éléments optiques principaux :
- l'objectif ( miroir concave convergent M1 à courbure parabolique; focale 6000 mm ; diamètre 480 mm ; grossissement maxi théorique : 2000 ) ;
- le miroir secondaire plan M ;
- l'oculaire, lentille convergent L.
Le télescope est considéré comme afocal.
Etude du miroir sphérique.
Définir la distance focale d'un miroir concave.
La distance focale d'un miroir sphérique est la moitié de son rayon de courbure.
Construire l'image A1B1 par le miroir, de la planète Uranus située à l'infini.
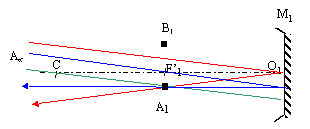
Uranus étant à
l'infini l'image A1B1 se trouve dans le plan
passant par F'1, perpendiculaire à l'axe de M1.
Tout rayon
passant par le centre C du miroir concave n'est pas dévié, il revient
sur lui même.
Tout rayon
passant par le foyer F'1 est réfléchi parallèlement à l'axe
optique principal du miroir.
Tout rayon
passant par le sommet O1 du miroir est réfléchi
symétriquement par rapport à l'axe optique principal du miroir.
Dmension de
l'image A1B1 : tan a ~ a = B1F'1
/ O1F'1.
Etude du miroir secondaire plan.
On note A2B2 l'image donnée par ce miroir plan.
A1B1 joue le rôle d'objet pour le miroir plan M.
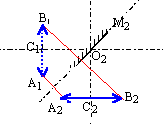
A1 et A2
sont symétriques par rapport au plan du miroir M2.
De même pour B1
et B2 et C1 et C2.
Oculaire.
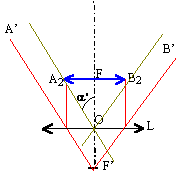
Si l'image
définitive A'B' est à l'infini alors A2B2 ,
jouant le rôle d'objet pour la lentille L est dans le plan focal objet
de L.
|
| .
. |
|
|
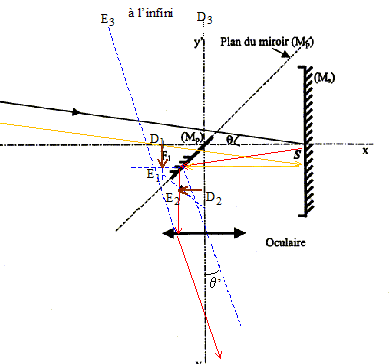
D1E1 en
fonction de q et f'1 : triangle SD1E1:
tan q = D1E1/ SF1
; tan q ~ q
d'où q = D1E1/ SF1
= D1E1/ f'1 .
q ' en fonction de D2E2
et f '2 : D1E1 = D2E2 et
tan q'
= D2E2/ f '2 ; tan q' ~ q' d'où q' = D2E2/ f '2
.
|
.
|
|
Le grossissement maximum du télescope, noté G, correspond au quotient de la distance focale de l'objectif f'1 par la distance focale de l'oculaire f'2 : G = f'1 / f'2.
Calculer f'2.
f'2 = f'1/G =6000 / 2000 = 3 mm.
G est aussi égal au quotient du diamètre apparent q' sous lequel est vu
l'astre à travers le télescope, par le diamètre apparent q sous lequel
l'astre est vu à l'oeil nu ( q = 1,07 10-3 degré).
Définir le diamètre apparent.
q = diamètre de l'astre / distance d'observation.
Calculer q' en degré.
q' = D1E1/ f '2 =q f'1/f'2 =qG =1,07 10-3 *2000 =2,14 °.
|
|
|



