Circuit RC.
Concours itpe 2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
Un
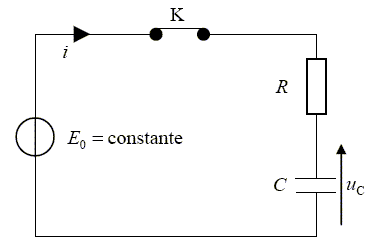
dipole comporte entre deux bornes A et B une résistance R et un
condensateur de capacité C placès en série. On place aux bornes A et B
du dipole un générateur de tension idéal de fem constante E0 et un interrupteur K.
Initialement le circuit est ouvert et le condensateur est déchargé. Soit uc la tension aux bornes du condensateur.
A l'instant t=0, on ferme l'interrupteur K.
Faire le schéma du circuit.
Quel est le comportement du condensateur au bout d'un temps très long après la fermeture de l'interrupteur ?
Le condensateur se comporte comme un interrupteur ouvert : uc=E0 et l'intensité du courant est nulle.
On pose t = RC.
Quelle est l'unité de t ? Démontrer ce résultat. Comment s'appelle cette constante ?
La constante de temps s'exprime en seconde.
R = U / I ( tension divisée par une intensité ) ;
C : charge divisée par une tension soit : intensité fois temps divisé par une tension.
RC a donc la dimension d'un temps.
Montrer que l'équation différentielle à laquelle obéit uc est de la forme : tduc/dt +uc = E0.
Additivité des tensions : E0 = R i + uc.
i = dq/dt = Cduc/dt ; E0 = R Cduc/dt + uc ; E0 = t duc/dt + uc .
Etablir l'expression de uc(t) en fonction de E0 et t. Retrouver la valeur de uc pour un temps très long.
Solution générale de l'équation différentielle sans second membre : u c(t) = A exp(-t / t) avec A = constante.
Solution particulière de cette équation ( régime permanent ) u c(t) = E 0.
Solution générale de cette équation : uc(t) = A exp(-t / t) +E0.
uc(0) = 0 =A exp(0) +E0 = A +E0 d'où A = -E0.
uc(t) = E0(1- exp(-t / t)).
Au bout d'un temps très long le terme en exponentiel est nul. uc(infini) = E0.
|
.
.
|
|
|
Donner l'allure de la courbe uc(t) en précisant son asymptote.
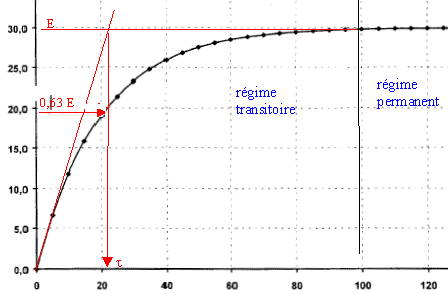
Asymptote uc(t) = E0.
L'abscisse de l'intersection de l'asymptote avec la tangente à l'origine donne la constante de temps.
|
.
|
|
Déterminer l'expression de l'intensité du courant i(t).
i = Cduc/dt = CE0 / t exp(-t / t)) = E0/R exp(-t / t)).
L'intensité décroît de manière exponentielle de E0/R à zéro pendant la charge du condensateur.
Déterminer en fonction de t l'expression du temps t1 à partir duquel la charge du condensateur diffère de moins de 1 % de sa charge finale.
uc(t1) = 0,99 E0 = E0(1- exp(-t1/ t)).
0,99 = 1-exp(-t1 / t) ; 0,01 = exp(-t1 / t) ; ln 0,01 = -t1 / t.
t1 =t (-ln0,01)=4,6 t.
|
|
|