Génie mécanique,
concours inspecteur
CCRF 2013
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
Déplacement d'un point matériel le long d'une came.
Un point matériel A est astreint à se déplacer, dans le plan Oxy, le
long du pourtour d'une came fixe. L'équation polaire de la came est r =
b - c cos q avec q = wt
. La tige qui permet le mouvement et réalise à l'aide d'un ressort le
contact sur la came, tourne uniformément autour de l'axe Oz, avec une
vitesse angulaire w.
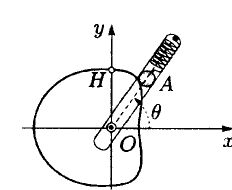
Donner l’expression du vecteur position OA dans le repère des coordonnées polaires planes (r,q)
Exprimer, en coordonnées polaires (r,q) , le vecteur vitesse du point matériel A
Exprimer, en coordonnées polaires (r,q) , le vecteur accélération du point matériel A.
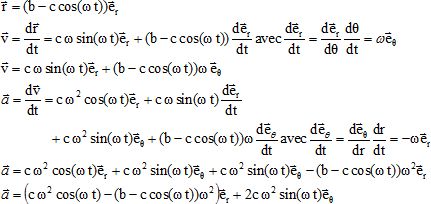
Calculer le module de la vitesse et de l'accélération, lorsque A atteint le point H de la came, sachant que w = 3,14 rad/ s , b = 2 cm et c =1 cm.
q = 90° ; cos 90 = 0 et sin 90 = 1.
Les composantes de la vitesse sont vH ( c w ; b w) soit : 0,01*3,14 et 0,02 *3,14.
vH =(0,03142 +0,06282)½ =7,0 10-2 m/s.
|
| .
. |
|
|
Les composantes de l'accélération sont aH( -b w2; 2c w2) soit :
(-0,02 *3,142 ; 0,02*3,142)
aH = 0,02*3,142 ((-1)2+12)½ =0,28 m s-2.
|
.
|
|
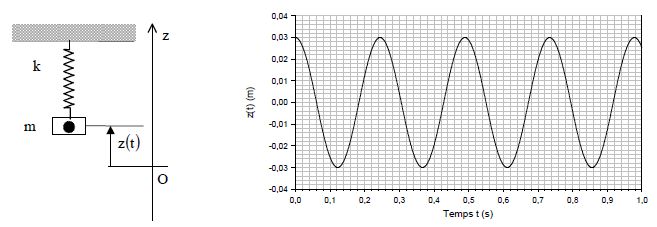
Système Masse – Ressort.
L'enregistrement de la position de la masse m du système de la figure 2 est décrit sur la figure 3.
Donner l’expression de l’équation différentielle caractérisant le
mouvement de la masse m ainsi que la solution de cette équation
différentielle et la dénomination des différents termes intervenants
dans la solution.
Ecrire la seconde loi de Newton sur un axe vertical dirigé vers le bas ; l'origine de
l'axe est la position d'équilibre stable du système masse ressort :
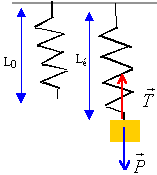
à l'équilibre : mg = k(Léq-L0)
|
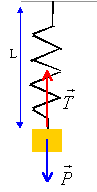
écarté de sa position d'équilibre le ressort
oscille : L= Léq +x
mg-k(L-l0)= m d²x/dt²
mg-k( Léq +x-l0)=
m d²x/dt²
mg-k( Léq -l0)
- kx =m d²x/dt² ; or mg = k(Léq-L0)
m
d²x/dt² + k x=0 (1)
|
Pulsation w0
( rad s-1) :
w0 = [k/m]½
d'où l'écriture de (1) : d²x/dt² + w20 x = 0 ou x" +w20 x
=0. (1)
La
solution de cette équation peut se mettre sous la forme x(t)=A cos(Bt) ou A et B sont des
constantes positives non nulles :
Calcul de B pour que x(t)=AcosBt soit solution de l'équation
différentielle.
dériver deux fois par rapport au temps : x' = AB (-sin (Bt) ; x" = -AB2cos(Bt)
repport dans (2) : -AB2cos(Bt) + w20A cos(Bt)
=0 ; B=w0
D'après le graphe, l'amplitude vaut 0,03 m ; x(0) = 0,03 = A cos (0) = A ; par suite x(t) = 0,03 cos (w0t).
|
A partir du graphique (figure 3), déterminer l'amplitude, la période,
la fréquence, la pulsation propre, le déphasage et la constante de
raideur du ressort du système sachant que m=5 kg.
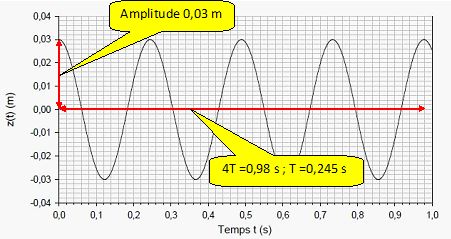
Fréquence f = 1/T = 1/0,245 =4,08 Hz ; pulsation w0 = 2 p f = 6,28*4,08 =25,64 ~25,6 rad/s.
La phase à l'origine est égale à zéro.
w02 = k/m ; k = m w02 = 5*25,642 =3,29 103 N/m.
|
|
|