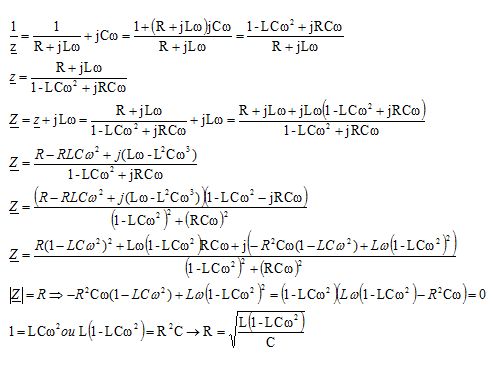Une
charge électrique de valeur q=1 C est disposée à chaque sommet d'un
carré de côté 2½m d'après le schéma
ci-dessous.
Calculer
le champ électrostatique et le potentiel au centre du carré.
On rappelle que leur expression fait intervenir une constante dépendant
du système d'unité que l'on se contentera ici d'appeler k sans la
détailler.
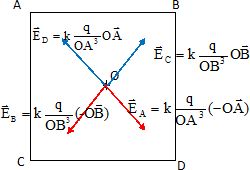
Par raison de symétrie, le champ électrostatique créé par les 4 charges
est nul au centre du carré.
Le champ dérive d'un potentiel : ce dernier est constant au centre O.
Potentiel créé par l'une des charges au centre O : V = k q / OA
avec OA =m.
Potentiel créé en O par les 4 charges : V = 4k/m.
Un conducteur filiforme de longueur L est
traversé par un courant de I=1 A lorsqu’on le relie à une source de
tension
de U=10V. Quelle
serait la valeur du courant si le conducteur avait la même longueur
mais un diamètre 2 fois plus grand ?
La résistance électrique d'un fil est inversement proportionelle à sa
section. Si le diamètre du fil double, la section quadruple et en
conséquence la résistance électrique est divisée par 4.
La tension U étant constante, l'intensité quadruple et vaut 4 A.
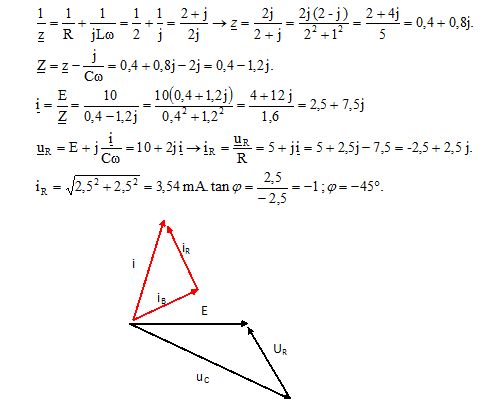
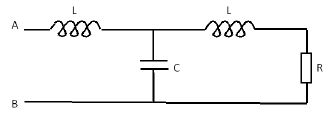
On alimente le circuit
ci-dessous à l'aide d'un générateur de tension sinusoidale e de
fréquence f et d'amplitude E.
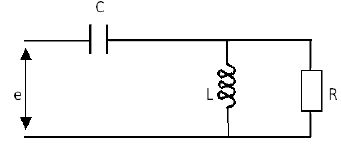
Calculer
à l’aide du théorème de Thévenin l’amplitude et le déphasage du courant
circulant dans la résistance R.
On donne : L =
10-3H ; C = 0,5 10-9F ; R = 2kW ; f = 106/2π
Hz; E = 10 V.
Les grandeurs soulignées sont des nombres complexes.
z
: impédance complexe de la portion L R en dérivation ; Z : impédance totale.
i :
intensité dans le circuit principal ; iR : intensité
dans R ; uR
tension aux bornes de R.
A la tension e = E sin ( wt)
on associe le nombre complexe e
= E. La phase de e est prise comme origine des phases.
w = 2 p f =106 rad/s ; Lw = 10-3 *106
= 103 ohms = 1 kW
; 1/(Cw) =1/(0,5 10-9
*106)= 2 103 ohms = 2 kW