Thermomètre à
résistance métallique, photodiode, concours inspecteur CCRF 2013
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
On veut
réaliser des mesures de température au moyen d’un thermomètre à
résistance métallique. En première approximation, la résistance R d’un
conducteur varie en fonction de la température selon la relation :
(1) R = R0(1+aq)
R0 est la résistance du conducteur à q0 = 0°C
a est le
coefficient de température en °C-1.
Expliquer
le principe du thermomètre à résistance métallique.
La
résistance électrique d'un conducteur métallique croît avec la
température. Cette variation de résistance est réversible. Comme métal,
on peut utiliser l'or, le cuivre, le nickel ou le platine. Les sondes de platine Pt100 présentent l'avantage de
posséder une bonne linéarité.
La sonde Pt100 ( symbolysée par le conducteur
ohmique de résistance R Pt) est insérée dans le montage
suivant :
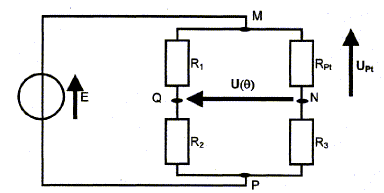
L'intérêt de ce circuit est de convertir une information
" résistance" en information "tension". Puis cette information sera
affichée directement en °C.
Influence du
métal sur la sensibilité.
Parmi les critères de performance d’un appareil de mesure figure
la sensibilité. Celle-ci est définie comme la variation de la grandeur
de sortie S obtenue pour une variation infinitésimale de la grandeur
mesurée G.
Exprimer
la sensibilité s en fonction de S et G. Appliquer cette
définition au cas d’un thermomètre àrésistance métallique (on supposera
a constant).
s = dS/dG =dR / dq
=aR0.
On rappelle que la résistance d’un conducteur de résistivité r, de section s et de longueur L
estdonnée par la relation :
(2) R = r L/s.
En considérant les relations (1) et (2), comment choisir le
métal de façon à optimiser la sensibilité.
La résistivité et le coefficient de température doivent être grands. La
linéaité doit être conservée.
Étude
d’un thermomètre à résistance métallique.
On a mesuré la résistance d’un thermomètre à résistance métallique pour
différentes températures :
q(°C)
|
10
|
30
|
50
|
70
|
90
|
R(ohm)
|
104
|
112
|
120
|
127
|
135
|
Tracer R = f(q). En déduire R0 et a. Quelle est la
sensibilité du thermomètre ?
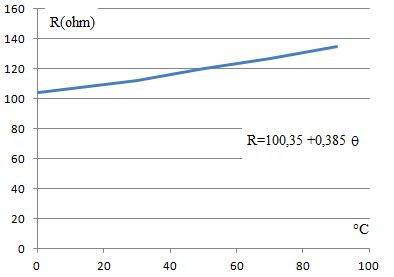
R 0~100
ohms ; a R 0=
0,385 ohm °C -1. a
= 0,385/100 = 3,85 10 -3 °C -1. Sensibilité s
= 0,385 ohm °C-1.
|
| .
. |
|
|
On étudie le
temps de réponse du thermomètre à résistance métallique précédent, lors
de la mesure de température d’un liquide. Les dimensions du thermomètre
sont négligeables par rapport à celles du liquide. La capacité
thermique massique (ou chaleur massique) du métal constituant le
thermomètre est C.
Le thermomètre, de température T0, est plongé dans le
liquide, de température T1 inférieure à T0.
Exprimer
le transfert thermique en fonction de la variation infinitésimale de
température dT.
dQ = CdT.
Du point de vue cinétique, on suppose que le transfert thermique,
pendant la durée dt, entre un corps de température T et le milieu de
température T1 suit la relation : dQ = ß.(T-T1).dt
Établir
l’équation différentielle vérifiée par T, puis la résoudre.
ß.(T-T1).dt + CdT =0
; dT/(T-T1)
=-ß/C dt.
ln(T-T1) =-ß/C
t + cste.
A l'instant t=0, T = T0 : cste = ln(T0-T1)
; ln((T-T1)/ (T0-T1) )=-ß/C
t.
T-T1= (T0-T1)
exp(-ß/C t) ; T = T1+ (T0-T1)
exp(-ß/C t).
|
.
|
|
On
relève la température au cours du temps :
t(s)
|
0
|
3
|
5
|
10
|
20
|
40
|
70
|
T(K)
|
330,0
|
314,2
|
306,5
|
294,1
|
283,3
|
280,3
|
280,0
|
Tracer
T = f(t).
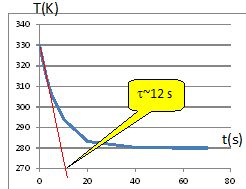
En
déduire les valeurs de T0 et T1. Définir une
constante de temps et l’évaluer.
T0 = 330 K ; T1 = 280K.
L'équilibre thermique est atteint au bout d'une durée proche de 5 fois
la constante de temps. La constante de temps est proche de t=12 s.
Dans le cas d'une variation exponentielle, la constante de temps est
donnée par l'abscisse de l'intersection de la tangente à l'origine avec
l'asymptote horizontale.
On donne ß = 16,5 J.K-1.kg -1.s-1.
Calculer
C.
t = C /ß ; C = ß t ~16,5*12 ~ 200 J.K-1.kg
-1.
On donne les propriétés de quelques métaux dans le tableau suivant :
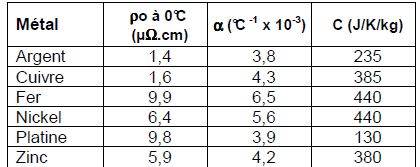
Quel
métal a été utilisé pour fabriquer la sonde du thermomètre, sachant
qu’il s’agit de l’un de ceux indiqués ci-dessus ?
L'argent, suivi du platine : a
et ß sont les plus proches des valeurs calculées.
|
Une
photodiode est un dipôle non linéaire dont la principale
caractéristique est de convertir l’énergie des photons en un courant
électrique. Ce dernier, appelé photo-courant ou courant photo-induit,
s’additionne au courant inverse de la jonction lié aux porteurs
minoritaires. Ce photo-courant est, dans certaines conditions,
proportionnel au flux rayonnant F
reçu par la diode et sera supposé comme tel dans tout le problème. Il
varie entre 1 μA et quelques mA. La
photodiode peut être utilisée notamment dans la réalisation de
détecteurs de lumière ou comme générateur de courant. Son schéma
conventionnel est le suivant :
On rappelle que la
caractéristique courant - tension iD = f(uD)
d’une diode simple (ou d’une photodiode dans l’obscurité) est, en
convention récepteur :
iD = IS.(exp( q.uD / (kT)) - 1) = IS.(exp(
uD / Y) - 1)
où k est la constante de Boltzmann, T la température absolue et q la
charge élémentaire de l’électron. IS est l’intensité du
courant inverse traversant la diode lié aux porteurs minoritaires.
Montrer
que la caractéristique i = f(u) de la photodiode peut s’écrire
(toujours en convention récepteur) i = IS.(exp( (u / Y)) - 1) - Iph , où Iph
est l’intensité du photo-courant. Représenter l’allure de
cette caractéristique pour un flux rayonnant non nul.
Le photo-courant s’additionne au
courant inverse de la jonction lié aux porteurs minoritaires.
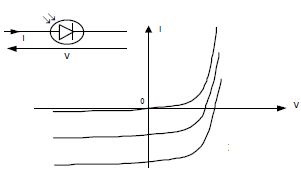
Photodiode
polarisée en inverse (u < 0).
Montrer
que pour les tensions habituelles de quelques volts (en valeur
absolue), i peut s’écrire : i = - (IS + Iph).
i = IS.(exp( (u / Y)) - 1) - Iph : u/Y est négatif et en valeur absolue bien supérieur à 1 : le terme en exponentiel est donc proche de zéro et i = - (IS + Iph).
Donner une expression
approchée de i sachant que IS est de l’ordre du nanoampère.
Le photo-courant varie de 1 µA à quelques mA. IS est de l’ordre du nanoampère : i ~-Iph.
En déduire que | i | = K.F avec K = constante et F flux rayonnant reçu
par la photodiode (en W).
Ce photo-courant est, dans certaines conditions,
proportionnel au flux rayonnant F
reçu par la diode. |
|
|
Étude d’une photopile.
On considère une cellule photovoltaïque (ou photopile), constituée
d’une photodiode telle que définie à la question 1, et utilisée avec
des valeurs de u positives et des valeurs de i négatives.
Montrer que dans ces conditions, la photodiode se comporte comme un générateur.
La puissance P = u i est négative : le dipôle ne consomme pas de
puissance mais au contraire peut en fournir : c'est un générateur.
Établir que la caractéristique de cette photopile peut s’écrire : i = IS.(exp(
uD / Y) - 1) - a.F avec : F flux rayonnant reçu par la photopile ; a coefficient de proportionnalité entre le photo-courant et le flux reçu.
i = IS.(exp( (u / Y)) - 1) - Iph avec IpH proportionel au flux rayonnant reçu par la photodiode.
Calculer la tension à vide de la cellule uCO (circuit ouvert).
L'intensité est nulle : IS.(exp(
uCO / Y) - 1) - a.F =0 ; exp(
uCO / Y) - 1= aF /IS ; exp(
uCO / Y) = 1+aF /IS ;
uCO / Y = ln(1+aF /IS) ; uCO =Y ln(1+aF /IS)
Faire l’application numérique pour un ensoleillement E de 500 W/m². Données : IS = 0,25 nA ; Y = 26 mV ; a = 0,3 A/W ; S surface utile de la photopile = 10 cm².
Y = 2,6 10-2 V ; IS = 2,5 10-10 A ; F = ES = 500*10*10-4 =0,5 W.
uCO =2,6 10-2 ln (1+0,3*0,5 /(2,5 10-10))= 0,228 ~0,23 V.
Dans la suite du problème, on conservera cette valeur de l’ensoleillement (correspondant à un temps moyennement ensoleillé)
Calculer le courant de court-circuit iCC.
u=0 ; iCC = IS.(exp( 0 / Y) - 1) - a.F = -a.F = -0,3*0,5 = -0,15 A.
Établir la relation vérifiée par u lorsque la puissance fournie par la cellule est maximale (P=PM). Soit uM cette valeur de u.
NB : On considèrera que, dans ces conditions, u >> Y.
exp(
uD / Y)-1 ~ exp(
uM / Y) ; i = IS.exp(
uM / Y) - a.F ; exp(
uM / Y) = i / IS+ a.F ;
uM = Y ln( i / IS+ a.F).
Vérifier, en utilisant la dérivée seconde de P par rapport à u, que PM est bien un maximum.
P = u(- i)= -u [IS.(exp(
uD / Y) - 1) - a.F]
Dérivée première par rapport à u : -[IS (exp(
uD / Y) - 1) - a.F + u IS/ Y exp(
uD / Y)] ;
Dérivée seconde par rapport à u : -[IS/ Y exp(
uD / Y) +IS/ Y exp(
uD / Y)+u IS/ Y exp(
uD / Y)]=-IS/ Y exp(
uD / Y)(2+u).
La dérivée seconde étant négative la courbe est convaxe il s'agit d'un maximum.
Par dichotomie, trouver la valeur numérique de uM sachant que celle-ci est comprise entre 0,4 et 0,5 V. En déduire la valeur de l’intensité correspondante iM.
La dérivée première s'annule et change de signe en présence d'un extrémum.
IS (exp(
uM / Y) - 1) - a.F + uM IS/ Y exp(
uM / Y) =0 ; IS (exp(
uM / Y)(1+uM)-IS-aF=0.
2,5 10-10 (exp(
uM / 0,026)(1+uM)-2,5 10-10-0,15=0.
2,5 10-10 (exp(
uM / 0,026)(1+uM)-0,15~0.
exp(
uM / 0,026)(1+uM) =0,15 /(2,5 10-10) ~6 108.
Pour uM = 0,43 : exp(
uM / 0,026)(1+uM) =2,17 107. Pour uM = 0,5 : exp(
uM / 0,026)(1+uM) =3,37 108.
Pour uM = 0,51 : exp(
uM / 0,026)(1+uM) =5 108. Pour uM = 0,52 : exp(
uM / 0,026)(1+uM) =7,38 108.
Pour uM = 0,515 : exp(
uM / 0,026)(1+uM) =6,04 108.
uM = 0,515 V.
Or
uM = Y ln( iM / IS+ a.F) =0,026 ln( iM/(2,5 10-10) +0,15).
0,515/0,026 = 19,807 = ln( iM/(2,5 10-10) +0,15) ; e19,807 = 4,00 108 = iM/(2,5 10-10) +0,15.
iM = 0,10 A.
Le rendement de la cellule est le rapport r entre la puissance maximale fournie PM par la photopile et le flux rayonnant reçu. Calculer r pour un ensoleillement de 500 W / m².
PM = 0,10*0,515 = 5,15 10-2 W ; F =0,5 W ; r = 5,15 10-2/0,5 = 0,103.
|





