Mesure de la
distance focale d'une lentille, condition d'émergence d'un prisme :
concours CPR 2013
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
Mesure de la
distance focale d'une lentille convergente.
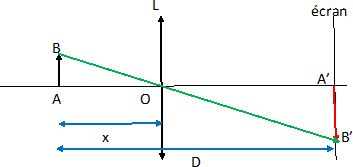
On projette sur un écran l'image nette A'B' donnée par une lentille
d'un objet lumineux AB.
Répondre
Vrai ou Faux.
L'épaisseur de la lentille est négligeable devant ses rayons de
courbures. Vrai.
L'image d'un objet réel donnée par la lentille est toujours réelle et
renversée. Faux.
La lentille peut
fonctionner en loupe.
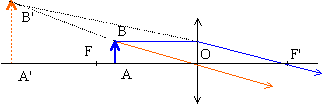
Dans l'approximation de
Gauss les rayons sont inclinés sur l'axe optique. Faux.
La lentille utilisée en loupe est un système convergent qui fait
croître le pouvoir séparateur. Vrai.
En dessous d'une
valeur minimale de D, notée Dmin, il n'existe plus de valeur
de x physiquement acceptable, correspondant à une image nette sur
l'écran.
La distance Dmin peut s'écrire
:
Dmin = f ' ; Dmin
=½ f ' ; Dmin
= 2f ' ; Dmin = 4f '. Vrai.
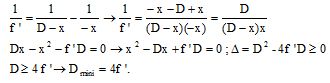
Pour D > D min il existe deux positions O 1 et O 2
de la lentille pour lesquelles une image nette se forme sur l'écran.
On pose d = O 1O 2. D = 1,00 m ; x 1 = AO 1
= 0,275 m ; x 2 = AO 2 =0,725 m.
La valeur de la distance
focale f ' est ( en cm) : 10 ; 15 ; 20 ; 25.
|
| .
. |
|
|
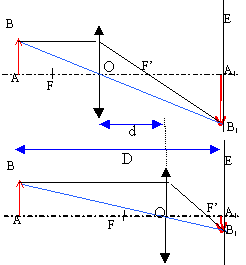
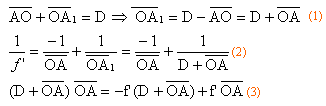
(2) réduction
au même dénominateur
Les dénominateurs étant égaux, il y a égalité entre les numérateurs. on
pose mesure algébrique de OA = x.
d'où en effectuant : D x +x² = -f' D -f' x + f' x
x² + Dx + f'D=0
résoudre l'équation du second degré :
D= D²-4f'D
le discriminant est positif si D >4f'
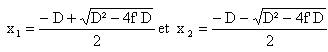
la différence x1-x2 est égale à d.
élever au carré d'où : d² = D²-4f ' D
soit (D²-d²) / (4D) = f '.
f ' = (1-0,452) / 4 ~ 0,20 m = 20
cm.
|
.
|
|
Condition d'émergence d'un prisme.
On éclaire un prisme ABC d'indice n par un faisceau de
lumière monochromatique. Le prisme est rectangle en B et l'angle ACB
vaut 45 °. Un rayon lumineux arrive perpendiculairement sur la face AB
en I.
La condition que doit vérifier n pour que le rayon incident subisse la réflexion totale sur la face AC est
:
n = racine carrée (2) ; n = 2 racine carrée (2) ; n > racine carrée (2) ; n < racine carrée (2).
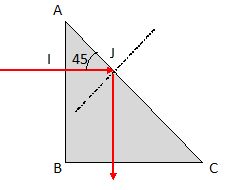
En J : n sin 45 = nair sin r ; n sin 45 = sin r ; il y a réflexion totale en I si n sin 45 > 1 ; n > 1/sin 45 ; n > racine carrée (2).
Sur la face AB du prisme arrivent perpendiculairement deux faisceaux monochromatiques de longueur d'onde respectives l1 et l2 ; n1 = 1,41 pour la lumière l1 ; n2 = 1,47 pour la lumière l2.
La lumière l1 se réfléchit totalement sur la face AC. Faux.
La lumière l2 se réfléchit totalement sur la face AC. Vrai.
L'angle d'émergence est i' = 60°. Faux.
L'angle de déviation du rayon incident est D = 40,6°. Vrai.
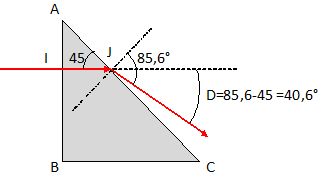
En J : n1 sin 45 = nair sin r1 ; sin r1 =1,41 sin 45 = 0,997 ; r1 = 85,6°.
En J : n2 sin 45 = nair sin r2 ; sin r2 =1,47 sin 45 = 1,039 ; r2 n'existe pas, il y a réflexion totale.
|
|
|