QCM mécanique, satellite, oscillateur, travail, énergie : concours
avenir 2013
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
Chaque bonne réponse est
gratifiée de 3 points, chaque mauvaise réponse est pénalisée d'un point.
Parmi les
affirmations suivantes, une seule est VRAIE. Laquelle ?
A)
Un mobile ne peut pas avoir un mouvement curviligne plan si son
accélération garde toujours la même direction.
B)
Un mobile ne peut pas avoir une accélération non nulle en un instant où
sa vitesse est nulle.
C)
Un mobile ne peut pas avoir une trajectoire curviligne si la direction
de la vitesse ne varie pas.
( Vrai
)
D)
Un mobile ne peut pas voir varier la direction de sa vitesse quand son
accélération est constante.
Voici le graphe d’une loi horaire
a(t), décrivant l’accélération d’un mobile au cours du temps. On
considère que le mobile ne peut se déplacer que suivant une direction,
repérée par l’axe (Ox), et qu’à l’instant t0 = 0
il est immobile en x0 = 0
.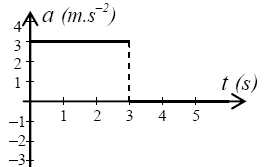
Quelle est l’affirmation qui coïncide avec la figure :
A)
La vitesse diminue linéairement à partir de l’instant t = 3s.
B)
Le mobile a une vitesse constante à partir de l’instant t = 3s.( Vrai ).
C)
Le mobile ralentit à partir de l’instant t = 3s et s’arrête.
D)
Le mobile ralentit à partir de l’instant t = 3s et repart dans l’autre
sens.
v(t) = 3t
entre 0 et t=3 s; v=constante = 9 m/s à t > 3 s.
Durant les
3 premières secondes du mouvement, la loi horaire de la vitesse est :
A)
v(t)=
3t.( Vrai ) B) v(t) = 1,5(t+3). C) v(t) = 3 t-9. D) v(t)=3(t+3)+9.
Dans le champ de pesanteur uniforme g0
= 10 m.s–2, une boule en fer de masse m = 700 g
est lancée vers le haut à t = 0, depuis le niveau z0
= +1 m, avec une vitesse initiale v0 = –4 m.s–1.
On supposera dans cet exercice que l’on peut négliger les frottements
de l’air.
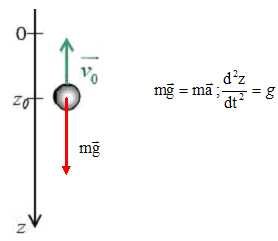
On étudie le mouvement vertical de la boule.
L’équation différentielle du mouvement est :
A)
d2z/dt2 +g/m z = Pm/v0
( P est le poids de la boule ). B) d2z/dt2
=g/m z
C)
d2z/dt2
=P/m ( Vrai ) . D) d2z/dt2
=-g.
La loi
horaire décrivant la position de la boule au cours du temps, z(t), est :
A) z(t) = -½gt2+v0t+z0. B) z(t) = ½gt2-v0t-z0.
C)
z(t) = -½gt2+v0t. D) z(t) = ½gt2-v0t+z0.( Vrai ).
v(t) = gt -v0 ; z(t) = ½gt2-v0t+z0.
Soit tmax la
date à laquelle la boule atteint sa hauteur maximale. La
vitesse de la boule vaut à cet instant :
A)
0.( Vrai ). B) -1 m/s.
C)
-6 m/s. D) +2 m/s.
Au point le plus haut, la
composante verticale de la vitesse est nulle.
L’expression
de la date tmax est alors :
A) v0/g.( Vrai ). B) (2v0/
(g-v0z0))½.
C)
(2v0/
(g-v0z0))½-z02/g. D) (2v0/
(g-v0z0))½-z02/g.
v(tmax)
= gtmax -v0 =0 ; tmax =v0 /g.
L’expression
de la hauteur maximale zmax atteinte par la
boule est :
A) ½v02/g+z0. B) ½v02/g-z0. C) -½v02/g-z0. D) -½v02/g+z0.( Vrai ).
zmax = ½g(v0 /g)2-v0(v0
/g)+z0 = -½v02/g+z0.
|
| .
. |
|
|
Le
mouvement d'un satellite géostationnaire doit avoir :
A)
une période de rotation propre égale à la période de révolution de la
Terre autour du Soleil.
B)
une période de révolution égale à la période de rotation propre de la
Terre. ( Vrai ).
C) une période de
rotation propre qui dépend de son altitude.
D)
une période de rotation propre égale à un jour sidéral.
Un satellite doit
être mis en orbite circulaire autour de la Terre avec une période de
révolution T. Un certain nombre de grandeurs étant alors
fixées, on peut encore choisir :
A) l'altitude.
B) la vitesse.
C) l’accélération
angulaire propre.
D) le plan dans
lequel se situe la trajectoire.( Vrai ).
Deux
planètes sont en rotation autour du Soleil, la planète P1
est plus éloignée du Soleil que la planète P2.
En faisant l'approximation que leur trajectoire est circulaire, on montre
que :
A)
la vitesse de P1 est inférieure à celle de P2.( Vrai ).
B) la vitesse de P1
est supérieure à celle de P2.
C)
les vitesses de P1 et de P2
peuvent être égales.
D)
cela dépend de leurs masses.
v = (GM/r)½ avec r rayon de l'orbite, M :
masse de l'astre central.
Si
une planète a une trajectoire elliptique,
A)
la direction, le sens et la norme du vecteur vitesse restent constants.
B)
la norme du vecteur vitesse est constante.
C)
la norme du vecteur accélération est constante.
D) la norme du
vecteur accélération ne dépend pas de la masse de la planète. ( Vrai ).
a = GM/r2, avec M : masse de l'astre
central et r : distance du centre de la planète au centre de
l'astre central.
|
.
|
|
Dans un manège
de foire en rotation rapide à vitesse angulaire constante, on emporte
un pendule simple pour faire quelques expériences à bord de la nacelle.
La position d’équilibre du pendule est :
A)
verticale parce que le poids n’a pas changé de direction.
B)
inclinée parce qu’il apparaît une force d’inertie dans le référentiel
du manège.( Vrai ).
C) verticale tant
que le pendule est au repos.
D)
inclinée parce que dans le référentiel lié au manège le pendule n’est
jamais au repos.
Un pendule est écarté
d’un angle de 15° par rapport à la verticale. Au cours de ses
oscillations, son amplitude diminue régulièrement de 3° à chaque
oscillation. Quelle
est l’affirmation vraie :
A)
Le régime est sur-critique.
B)
Le régime est apériodique.
C)
Le pendule est amorti par des frottements solides.( Vrai ).
D) La pseudo-période
des oscillations diminue progressivement.
Un
dispositif solide-ressort peut coulisser sans frottements le long d’une
tige verticale.
Lorsqu’on écarte le solide de sa position d’équilibre, la
résultante des forces extérieures appliquées sur le solide est
:
A)
nulle.
B)
égale à la tension du ressort seule, comptée par rapport à la position
d’équilibre.( Vrai ).
C) égale à la
tension du ressort seule, comptée par rapport à la position à vide.
D)
égale au poids du solide.
De quoi
dépend l’amplitude du mouvement de l’oscillateur non amorti
?
A)
de la raideur k du ressort.
B)
de la masse m du solide.
C)
de la phase f
à l’origine des dates.
D)
des conditions initiales du mouvement.( Vrai ).
Un oscillateur est
constitué d’un dispositif solide-ressort.
La
période propre des oscillations de l’oscillateur non amorti est
:
A) T0=(k/m)½.
B) T0=(m/k)½.
C) T0=2p(k/m)½.
D) T0=2p(m/k)½.( Vrai )
Une masse de 1000 kg est suspendue au bout d’un ressort vertical.
Sachant que l’on veut obtenir des oscillations de période propre égale
à 1 seconde, la
raideur du ressort doit être environ :
A)
50 Nm-1. B)
1300 Nm-1. C)
7 kN m-1. D)
40 kN m-1.( Vrai ).
k =4p2m/T02 ~ 40*1000/12 =40 kN m-1.
|
Une bille de masse m = 50 g
peut glisser dans un bol de forme hémisphérique de rayon intérieur R =
10 cm. Elle est alors soumise à une force de frottements que l’on
supposera constante, de valeur F = 10 mN.
À l’instant
initial, la bille est lâchée sans vitesse initiale depuis un point A
tel que l’angle que fait la direction (OA) avec la verticale (OB) est
un angle droit. On
prendra pour le champ de pesanteur : g = 10 m.s–2.
Quel est
le travail WP du poids
de la bille sur le trajet de A à B ?
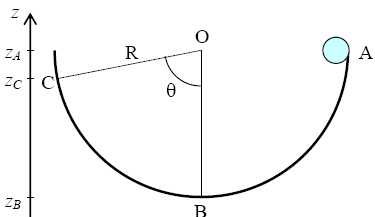
A)
-60 mJ. B) -20 mJ. C) +50 mJ.( Vrai ). D) +120 mJ.
En
descente le travail du poids est moteur ; le travail d'une force
constante ne dépend pas du chemin suivi mais uniquement des positions
initiale et finale.
Wp = mg(zA-zB) =mgR =0,050*10*0,1 =0,050 J = 50 mJ.
Quel est le travail Wf de la force de frottements au cours du trajet de la bille de A à B ?
(indication : la longueur d’un arc de cercle d’angle a et de rayon R est L = aR, avec a en radians : 90° = 1,5 rad).
A)
-150 mJ. B) -1,5 mJ.( Vrai ). C) +30 mJ. D) +150 mJ.
Le travail des frottements est résistant.
Wf =-F R a =-0,010*0,10*1,5 =-1,5 10-3 J = -1,5 mJ.
On suppose maintenant que l’énergie potentielle de la bille est nulle au point B. L’énergie mécanique de la bille en A est :
A) 1,5 mJ. B) 30 mJ. C) 50 mJ.( Vrai ). D) 80 mJ.
En A l'énergie mécanique est sous forme potentielle de pesanteur : mgR =0,050*10*0,10 =0,050 J = 50 mJ.
L’énergie cinétique de la bille quand elle passe en B est :
A) 1,5 mJ. B) 48,5 mJ.( Vrai ). C) 50 mJ. D) 51,5 mJ.
Entre
A et B, l'énergie mécanique diminue du travail des frottements ; en B
l'énergie mécanique sera sous forme cinétique : 50-1,5 = 48,5 mJ.
|
|