Propriétés de l'ammoniac et de ses composés : concours assistant d'ingénieur 2013 En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts. . . Atomistique. Etablir la configuration électronique et le schéma de Lewis de l’atome d’azote. Quelle est sa valence ? 1s2 2s2 2p3. Il y a trois électrons externes célibataires ( valence 3) et un doublet non liant. Etablir le schéma de Lewis des édifices suivants. Représenter dans l’espace les édifices et nommer la répartition des doublets électroniques autour de l’atome central lorsqu’il existe. Comparer les angles observés dans NH3 et NH4+. Justifier. Dans l'ion ammonium la symétrie tétraèdrique donne des angles de 109°. Dans la molécule d'ammoniac, le doublet non liant repousse les doublets de liaison : les angles sont proches de 107°. Quelle particularité présentent les schémas de NO3- et de NO2- ? Illustrer sur NO2-. On peut écrire plusieurs structure de résonance. Fabrication industrielle de l’ammoniac. A partir de quels réactifs est obtenu l’ammoniac industriellement ? Le dihydrogène et le diazote. Présenter rapidement les étapes de la synthèse industrielle de l’ammoniac actuelle la plus courante. On pourra s’aider des équations chimiques. Le diazote est fourni par l'air et le dihydrogène par vaporeformage du méthane, gaz naturel. CH4 + H2O --> CO + 3H2. CO + H2O --> CO +H2. N2+3H2 --> 2NH3 en présence d'un catalyseur à base de fer. Comment l’ammoniac est-il récupéré en fin de synthèse ? L'ammoniac est récupéré sous forme liquide. Citer un autre réactif industriel synthétisé à partir de l’ammoniac. L'ammoniac est urilisé principalement dans la formation d'engrais azotés. L'oxydation de l'ammoniac en présence d'eau et de dioxygène conduit à l'acide nitrique. . . Utilisation d’une solution commerciale d’ammoniac. La FDS associée à un flacon commercial d’ammoniaque à 25 % indique d = 0,903, M = 17 g.mol-1. Déterminer littéralement puis numériquement la concentration molaire de cette solution. Masse de 1 L de solution commerciale 903 g. Masse d'ammoniac pur : 903*0,25 =225,7 g Concentration molaire : 225,7 / 17 =13,3 mol/L. Quel volume de cette solution faut-il utiliser pour fabriquer 1L d’ammoniaque à environ 0,1 mol.L-1 ? Facteur de dilution : 13,3 / 0,1 = 133 ; volume de solution commerciale à prélever : 1000 / 133 =7,5 mL. La concentration de la solution commerciale étant approximative, expliquer comment vous procédez pour préparer à partir de cette solution une solution ajustée à 0,1 mol.L-1. On ne demande pas de calcul mais une méthode que vous pourriez transmettre à un adjoint technique. Doser la solution d'ammoniac avec une solution d'acide chlorhydrique de concentration connue avec certitude. Ce dosage permet de connaître la concentration précise de la solution d'ammoniac. Ajouter alors de l'eau distillée si la solution d'ammoniac est trop concentrée ou de l'ammoniac du commerce si la solution est trop diluée. Puis effectuer un nouveau dosage avec la solution d'acide chlorhydrique de concentration connue pour vérification. . Cristallographie. En dessous de 184°C, le chlorure d’ammonium solide cristallise avec une structure de type CsCl, de paramètre de maille a = 387 pm. L’ion ammonium est supposé sphérique. Représenter la maille élémentaire et la nommer. Identifier le motif. Quelle est la coordinence de chaque ion ?   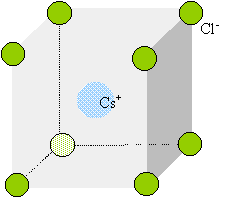Structure cristalline cubique. Chaque ion NH4+ est équidistant de 8 ions chlorures. Chaque ion Cl- est équidistant de huit ions NH4+. La coordinence est égale à 8. Calculer la masse volumique de ce solide sachant que sa masse molaire est de 53,5 g.mol-1. Volume de la maille élémentaire : V =a3 =(387 10-12)3 =5,796 10-29 m3. Chaque maille élémentaire compte un ion ammonium et un ion chlorure; la masse de la maille est égale à : 53,5 /(6,021023) =8,887 10-23 g = 8,887 10-26 kg. Masse volumique : 8,887 10-26 /(5,796 10-29) =1533 ~1,53 103 kg m-3. Evaluer le rayon ionique de l’ion ammonium supposé sphérique sachant que, dans ce cristal, le rayon de l’ion chlorure est R = 187 pm. Les ions sont tangents suivant la grande diagonale du cube. 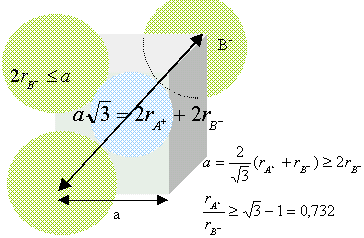RNH4+ +RCl- = 387*1,732 / 2 =335 pm ; RNH4+ =335-187 =148 pm. En déduire la compacité du chlorure d’ammonium. Volume des ions supposés sphériques : 4/3 p(R3NH4+ +R3Cl- ) =4*3,14 / 3(1873 +1483) (10-12)3 =4,097 10-29 m3. Compacité = volume des ions / volume de la maille = 4,097 10-29 / (5,796 10-29) ~0,71. On réalise un diagramme de poudre sur ce solide. Pour quel angle q obtient-on un maximum de signal correspondant à des plans atomiques séparés par le paramètre de maille a sachant que l’on éclaire la poudre avec la raie Ka du cuivre (l = 0,154 nm) ? Lorsqu'un faisceau monochromatique arrive sur un cristal en faisant un angle q avec une famille de plans réticulaires, il est diffracté. Un maximum d'intensité se produit lorsque les rayons diffractés sont en phase. Loi de Bragg : 2 d sin q = n l avec n entier, ordre de diffraction et d : distance entre deux plans réticulaires consécutifs de la même famille. pour n = 1 et d = a : sin q = l / (2a) =0,154 / (2*0,387) =0,199 ; q =78,5°. .

menu