QCM Ondes, oscillateur, satellite, accélération, niveau d'énergie :
concours Advance 2012
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
.
.
|
|
|
|
|
Propagation
d'une onde sur une corde.
Une perturbation se propage le long d’une corde élastique.
À la date t=0 s, le front de l’onde quitte le point S (extrémité de la
corde). Le retard du point M par rapport au point S est de 50 ms et la
distance SM est de 2 m.
A. L’onde se propage
à la vitesse de 0,04 m.s-1. Faux.
v = 2 /
0,050 =40 m/s .
La vitesse de propagation dépend de la tension F de la corde selon la
formule : v = (F/µ)½, μ étant la masse
linéique de la corde en kg.m-1.
B.
La tension F peut s’exprimer en kg.m.s-2. Vrai.
F = µv2
; F s'exprime en kg m-1 m2s-2
soit kg m s-2.
C.
Si la vitesse de propagation est de 20 m.s-1 et
μ = 10 g.m-1 alors la tension F a pour valeur 4
N. Vrai.
F = 0,010 *202 =4 N.
On fixe un vibreur à l’extrémité de la corde tendue, une onde de
fréquence f = 25 Hz se propage le long de la corde à la vitesse v = 20
m/s.
D. La longueur
d’onde l
vaut 16 cm. Faux
l = v / f =20 /
25 =0,80 m.
E.
Un point M’ se trouve à 4,4 m de la source S. M et M' vibrent en phase.Vrai.
MM' = 4,4-2 = 2,4 m soit 2,4 /
0,8 = 3 longueurs d'onde.
M et M'
étant distants d'un nombre entier de longueur d'onde sont en phase.
Oscillations
horizontales.
Un pendule élastique est constitué d’un solide de centre d’inertie G,
de masse m= 500 g relié à un ressort de raideur
k= 5 N.m-1. Le solide peut coulisser sans
frottement sur une tige horizontale. À l’équilibre, le centre d’inertie
coïncide avec l’origine de l’axe. On donne : p2~10.
Le mouvement du solide est étudié dans le référentiel terrestre
considéré comme galiléen.
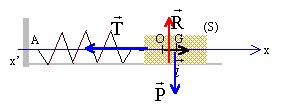
A.
L’équation différentielle du mouvement s’écrit : d2x/dt2-k/m
x = 0. Faux.
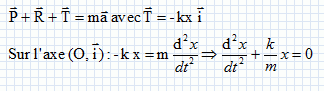 B. La période des
oscillations est T ≈ 20 s.Vrai.
T =2p(m/k)½
=6,28(5/0,5)½ ; T2 ~ 4
*10 *10 = 400 ; T ~20 s.
B. La période des
oscillations est T ≈ 20 s.Vrai.
T =2p(m/k)½
=6,28(5/0,5)½ ; T2 ~ 4
*10 *10 = 400 ; T ~20 s.
On écarte le solide de sa position d’équilibre telle que x = 2 cm puis
on le lâche sans vitesse initiale.
C.
À l’abscisse x = -2 cm, la tension F du ressort vaut 10 N. Faux.
F = k|x|
=5*0,02 = 0,10 N.
D.À
un instant t, x(t) = 1 cm. L’énergie cinétique a alors pour valeur Ec
= 7,5 10-4 J. Vrai.
Energie mécanique : E
= ½k x2max = 0,5*5*0,022
=1,0 10-3 J.
Energie potentielle élastique à l'instant t : ½k x2
= 0,5*5*0,012 =2,5 10-4 J.
Conservation de l'énergie
mécanique : Ec(t) = 1,0 10-3 -2,5 10-4 = 7,5 10-4 J.
E. À cet instant t,
l’énergie potentielle est nulle. Faux.
|
| .
. |
|
|
Satellite.
Un satellite artificiel est placé en orbite circulaire basse : le rayon
de sa trajectoire est : r1 = 6700 km, et sa
période T1 = 90 mn. On veut le faire passer en
orbite géostationnaire de rayon r2 = 42000 km et
de période T2 = 24 heures.
L'orbite de rayon r1 est un cercle de périmètre
: L1 = 2 p
r1 = 42100 km.
A.
La vitesse du satellite sur l'orbite de rayon r1
a pour valeur approchée v1 = 8 km/s. Vrai.
v1 = L1
/ T1 =42100 / (90*60)= 421/(9*6) ~420/(9*6) =
70/9 ~8 km/s.
B.
La vitesse v2 sur l'orbite géostationnaire
s'écrit : v2 = v1 (r2/r1)½.
Faux.
v1
=(GM/r1)½ ; v2 =(GM/r2)½
; M : masse de l'astre central.
v2/v1 = (r1/r2)½.
C. Entre les deux
trajectoires, la variation d'énergie cinétique s'écrit DEc
=½mv12(r1-r2)
/ r2. Vrai.
Ec1 = ½mv12
=½mGM/r1 ; Ec2 = ½mv22
=½mGM/r2 ; Ec2 -Ec1=½mGM(1/r2-1/r1).
or v12
=GM/r1 .
D.
Entre l'orbite géostationnaire et l'orbite basse, la variation
d'énergie potentielle s'écrit : DEp
= mv12(r1-r2)
/ r2. Vrai.
Ep1
=-mGM/r1 ; Ep2
=-mGM/r2 ; Ep1 -Ep2=mGM(1/r2-1/r1) = mGM / r1 (r1-r2)
/ r2 ; or v12
=GM/r1 ).
Pour faire passer le satellite de l'orbite basse à l'orbite
géostationnaire, il faut lui fournir l'énergie : DE=½DEp.
E.
Les grandeurs T1, r1, T2
et r2 vérifient la relation. T12r23
=T22r13 . Vrai.
La 3è loi de Kepler s'écrit
: T12/
r13= T22 /r23 = constante.
|
.
|
|
Vitesse
et accélération.
Le centre d’inertie d’un solide de masse m = 100 g est en mouvement. Il
possède, à chaque instant, les coordonnées suivantes dans un repère
orthonormé :
x(t) = 3t et y(t) = 4t2+6t.
A.
Le mouvement est rectiligne. Faux.
t = x/3 ; y
= 4x2/9 +6x/3 ; branche de parabole.
B.
À la date t=0, le centre d’inertie est à l’origine du repère. Vrai.
x(0) = 0 ; y(0) = 0.
C.
À la date t=0,5 s, v ≈ 10 m.s-1.
Faux.
vx = dx/dt = 3 m/s ; vy = dy/dt = 8t+6 ; vy(0,5) =10 m/s ; v = (32 +102)½ =10,4 m/s.
D.
L‘accélération est constante et vaut 4 m.s-2. Faux.
x" = 0 ; y" = 8 m s-2.
E. La valeur F de la
somme vectorielle des forces extérieures auxquelles est soumis le
solide vaut 0,80 N. Vrai.
F = ma =0,10 *8 = 0,80 N .
Onde
sonore.
La vitesse du son est vson = 340 m.s-1.
Un orage éclate et on entend le tonnerre 5 secondes après avoir vu
l’éclair.
A.
Une onde sonore se propage dans le vide. Faux.
B.
L’onde sonore est une onde transversale. Faux.
C.
Une onde sonore transporte de l’énergie. Vrai.
D. On se trouve à
1700 m de l’orage. Vrai.
5*340 = 1700 m.
E.
Le tonnerre se transforme parfois en un long grondement : c’est le
phénomène de diffraction. Faux.
|
Phénomène
de diffraction.
Un rayon laser, de longueur d’onde dans le vide λ= 600 nm traverse une
fente verticale de largeur a. On place un écran à une distance D = 3 m
de la fente.
Donnée : vitesse de la lumière : c= 3.108 m.s-1.
A.
Le faisceau est de couleur rouge. Faux.
600 nm
correspond au jaune.
B.
La fréquence de l’onde est de 5.1014 Hz. Vrai.
f =c / l = 3 108 / (600 10-9) =5.1014 Hz.
C. La figure de
diffraction obtenue est de direction verticale. Faux.
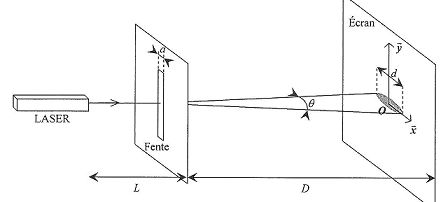
D. La largeur de la
tache centrale est L = 2
lD/a.
Vrai.
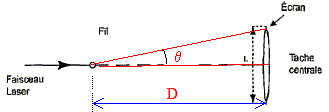
tan
q = ½L/D
voisin de q radian
pour les angles petits.
d'autre
part q
= l/a.
avec
: l longueur
d'onde (m) et a : diamètre du fil (m)
en
tenant compte des deux relations ci-dessus : ½L/D=l/a soit a=2lD/L ou L
= 2l
D/a.
E. On place l’écran
à 5 m. La figure ne change pas. Faux.
Niveaux
d’énergie d’un atome.
L’énergie
nécessaire à un atome pour passer de l’état fondamental à l’état ionisé
s’appelle l’énergie d’ionisation Ei.
Pour
l’atome d’hélium, Ei = 24,6 eV.
A. En admettant que
l’ion hélium He+ formé a une énergie
nulle, l’énergie de l’atome d’hélium dans son état fondamental est de
-24,6 eV. Vrai.
L’atome d’hélium se
trouve au niveau d’énergie E2 = -21,4 eV.
B. La longueur d’onde
de la radiation émise lors de la désexcitation vers l’état fondamental
se calcule par : l = (E2-E0)
/ (hc). Faux.
l = hc/(E2-E0).
C. l = 387 nm
est une radiation ultraviolette. Vrai.
Cette valeur
est inférieure à 400 nm.
D. L’atome peut
absorber toutes les radiations pour changer de niveau d’énergie. Faux.
L'énergie de
l'atome est quantifiée ; seules quelques valeurs sont permises.
E.
L’atome d’hélium, dans son état fondamental, est percuté par un
électron d’énergie 30 eV. Ce choc peut provoquer l’extraction d’un
électron avec une énergie maximale de 5,4 eV. Vrai.
|
|