Fission et fusion,
énergie solaire, dispositif de chauffage. Concours
technicien de l'industrie et des Mines
2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
Fission et
fusion.
Fission de
l'uranium.
23592U + 10n
--->139xXe + 9438Sr + y10n.
Déterminer
les entiers x et y.
Conservation du nombre de nucléons : 235+1 = 139+94+y, d'où y =3.
Conservation de la charge : 92 = x + 38, d'où x = 54.
Déterminer
l'énergie E, en joule puis en MeV, libérée par la fission d'un noyau
d'uranium 235.
Variation de masse Dm = m(139xXe)+m(9438Sr)+2m(10n)-m(23592U).
Dm =138,918 + 93,915
+2*1,009-235,044 = -0,193 u ou -0,193 *1,67 10-27 =-3,2231 10-28
kg.
E = Dm c2 = -3,2231
10-28 *(3 108)2 = -2,90
10-11 J ou -2,90
10-11 /(1,6 10-13) = -181 MeV.
En déduire l'énergie
libérée par la fission de 1,00 kg d'uranium 235.
Masse d'un noyau d'uranium 235 : 235,044*1,67 10-27 =3,925 10-25
kg.
Nombre de noyau dans 1,00 kg d'uranium 235 : 1,00 / (3,925
10-25)
=2,5476 1024.
Energie libérée : E'=-2,90
10-11 *2,5476
1024= -7,39 1013 J.
Fusion de
l'hydrogène.
L'hydrogène possède trois isotopes 11H, 21H
et 31H.
Ecrire
les différentes réactions qui, à partir de deux noyaux d'isotopes
identiques ou différents, conduisent à la formation d'un noyau d'hélium
accompagné ou non d'une ou plusieurs particules.
21H
+21H
---> 42He
; 11H
+31H
---> 42He
; 21H
+31H
---> 42He
+10n ; 31H
+31H
---> 42He
+210n.
On
s'intéresse à la réaction 21H
+31H
---> 42He
+10n.
Calculer
l'énergie E, en J puis en MeV, accompagnant la formation d'un noyau
d'hélium.
Dm =m(42He) +
m(10n) -m(31H) -m(21H)
=4,001+1,009-2,013-3,015 = -0,018 u
ou -0,018*1,67 10-27 = -3,006 10-29 kg.
E = Dm c2= -3,006
10-29 *(3
108)2 = -2,7054 10-12 J ou
-2,7054 10-12 /(1,6 10-13) =
-16,9 MeV.
Calculer
l'énergie libérée par la fusion d'une masse M = 1,00 kg de mélange
contenant le même nombre d'atomes des deux isotopes.
Masse des
isotopes : 2,013 +3,015 =5,028 u ou 8,3967 10-27 kg.
E' =-2,7054
10-12 /(8,3967
10-27) =
- 3,22 1014 J.
Cocher les cases du
tableau correspondant aux bonnes réponses.
|
Fission
|
Fusion
|
Plus
gande abondance des réserves de combustible
|
|
X
|
Production
moindre de déchets radioactifs
|
|
X
|
Pas
de risque d'emballement des réactions
|
|
X
|
Technologie
utilisée en production industrielle
|
X
|
|
.
|
| .
. |
|
|
Energie solaire.
On
considère que le soleil, lorsqu'il est visible, apporte en moyenne une
puissance de 750 W par m2 de surface horizontale. Le rendement du capteur
est 12%. Le soleil est visible 30 % du temps.
Déterminer l'énergie récupérable ER par mètre carré de
surface de capteur pour une année de 365 jours.
Energie
solaire : ER =750 *365*24*3600 *0,30
=7,0956 109 ~7,10 109 J m-2.
Energie électrique correspondante : 0,12 *7,0956
109 ~8,51 108 J m-2.
La consommation moyenne d'un habitant est évaluée à 2 t de pétrole par
an et 1 kg de pétrole fournit 4,2 107 J.
Calculer
l'énergie E consommée par habitant et par an.
E =2000*4,2 107
=8,4 1010 J.
Calculer
la surface de capteurs nécessaires pour alimenter en énergie une ville
d'un million d'habitants pendant un an.
106 E / ER =8,4 1016 / (7,10 109)
~1,2 107 m2.
En fait, l'ensemble des capteurs utilisés permet de recueillir en un
an, sous forme électrique, une énergie de 1,2 1017 J. Cette
énergie est transportée vers la ville par une ligne électrique sous une
tension de 200 kV efficace. le facteur de puissance est estimé à cos f = 0,95. Calculer la
puissance électrique.
Energie ( J) = puissance (W) / durée (s) ; P = 1,2 1017
/(365*24*3600) = 3,8 109 W.
En
déduire l'intensité efficace du courant.
I = P / (U cos f) =3,8 109
/( 2 105*0,95) =2,0 104 A. ( pour une ligne
monophasée ).
La ligne a une longueur totale de 40 km. On ne veut pas perdre plus de
10 % de l'énergie transportée par effet Joule.
Calculer
la résistance d'un kilomètre de ligne.
Energie maximale dissipée par effet Joule : EJ=0,10 *1,2 1017
= 1,2 1016 J.
Résistance de la ligne : EJ / (I2
t)=1,2 1016 /((2 104)2*365*24*3600)
=0,95 ohm.
soit 0,95 /40 = 2,4 10-2
ohm km-1. |
.
|
|
Dispositif de
chauffage.
On considère un dispositif de chauffage de l'eau d'une installation
industrielle. Captée à la température q1 = 15°C, l'eau doit
être chauffée à la température finale q2 = 85°C. Le
dispositif permet de chauffer M = 1000 kg d'eau par heure. Capacité
thermique massique de l'eau liquide c = 4190 J kg-1 K-1.
Le dispositif de chauffage comporte une chaudière qui produit en une
heure une masse m de vapeur d'eau à 100°C. Cette vapeur pénètre avec
l'eau à réchauffer dans un échangeur supposé strictement calorifugé.
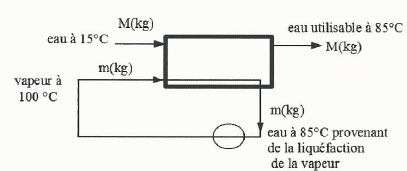
Calculer
la quantité de chaleur Qeau absorbée par 1000
kg d'eau dont la température passe de 15 °c à 85°C. En déduire la
puissance calorifique Peau reçue par l'eau à
réchauffer.
Qeau = Mc(q2-q1) =
1000*4190*(85-15)=2,933 108 ~2,9 108 J. Peau
= Qeau / durée = 2,933 108 /3600 =8,147 104
~8,1 104 W.
Donner
l'expression de la quantité de chaleur Q2 échangée par une
masse d'eau m provenant de la liquéfaction de la vapeur en passant de
la température q' = 100°C à
la température q2
= 85°C.
Chaleur latente de liquéfaction de la vapeur d'eau L = -2257,2 kJ kg-1.
Q2 = m L +mc(q2-q').
On considère le système formé par la masse d'eau M à réxchauffer et la
masse m de vapeur d'eau. On admet que la transformation est adiabatique.
En
déduire la masse m de vapeur d'eau nécessaire pour faire passer de 15°C
à 85°C la température de 1000 kg d'eau.
Qeau +Q2 = 0.
2,933 108 -m(
2257,2 103 +4190 *15) =0 ; m = 126,4 ~126 kg.
La chaleur est fournie par la combustion du fuel dans la chaudière.
Chaque kg de fuel brûlé donne une quantité de chaleur de 4,2 107
J. Le rendement de la chaudière est égal à 0,80.
Calculer
la consommation horaire de fuel.
Energie ( par kg de fuel ) utile à chauffer le
système : 4,2 107 *0,80 = 3,36 107 J kg-1.
Masse de fuel : Qeau /(3,36 107)
= 2,933 108 /(3,36 107
) =8,73 ~8,7 kg h-1.
|
|
|