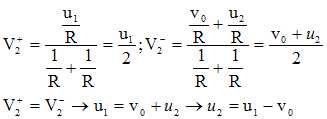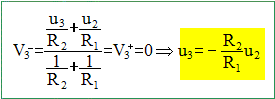Vidange
d'un bassin, séparation d'isotopes, capteur de température, cycle de
Brayton. Concours
technicien de l'industrie et des Mines
2014
En poursuivant votre navigation sur ce site, vous acceptez l’utilisation de Cookies vous proposant des publicités adaptées à vos centres d’intérêts.
|
|
.
.
|
|
|
|
|
|
|
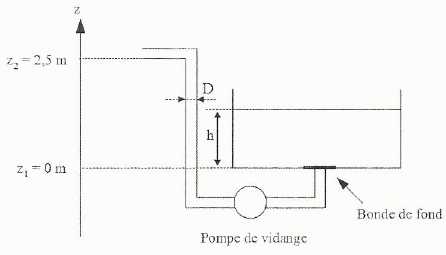
Vidange d'un bassin.
Le bassin est parallélépipédique de dimensions L = 4,0 m, d = 3,0 m et
h = 2,0 m. Le fluide est de l'eau de masse volumique r = 1,0 103 kg
m-3. La pression de l'air est P0 = 1,0 105 Pa. On prendra g = 10 m s-2.
Calculer le volume d'eau du bassin.
V = L d h =4,0 *3,0*2,0 =24 m3.
Calculer la pression P1 au fond du bassin au niveau de la bonde.
P1 = P0 + rgh = 1,0 105 + 1,0 103+10+2,0 = 1,2 105 Pa.
On désire vider le contenu du bassin en une durée Dt = 30 minutes en actionnant une pompe. La conduite de vidange débouche àl'air libre à une altitude z2 = 2,5 m au dessus du fond du bassin. On négligera pour cette partie les pertes de charge.
Calculer le débit volumique Dv de la pompe en m3 s-1 et en L s-1.
Dv = V / Dt = 24 /(30*60) =1,333 10-2~1,3 10-2 m3s-1 =13 L s-1.
Le diamètre de la conduite de vidange est D = 5,0 cm.
Calculer la vitesse d'écoulement de l'eau dans la conduite.
v = Dv/(pR2) =1,333 10-2/(3,14 (2,5 10-2)2) =6,7906 ~6,8 m/s.
On rappelle l'équation de Bernoulli dans une installation avec une pompe :
½r(v22-v12)+rg(z2-z1) +P2-P1 = Ppompe / Dv.
Déterminer la puissance de la pompe. On négligera v1 devant v2.
Ppompe =Dv(½r v22+rg(z2-z1) +P2-P1 )= 1,333 10-2( 500*6,792+1,0 104*2,5 +2,0 104)=9,07 102 ~9,1 102 W.
Séparation d'isotopes.
Un spectrographe de masse est constitué de plusieurs
parties comme l'indique la figure ci-dessous :
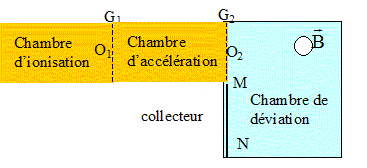 Dans la chambre d'ionisation les atomes d'uranium 23592U et 23892U de masses respectives m 1 et m 2 portés à haute température sont ionisés en ion U +. A la sortie de cette chambre, la vitesse des ions est quasi-nulle. Les ions sont accélérés entre O 1 et O 2 sous l'action d'une différence de potentiel établie entre les grilles G 1 et G 2. Les ions sont ensuite déviés par un champ magnétique uniforme. Une fente centrée sur O 2 de largeur L dans le plan de la figure permet de choisir la largeur du faisceau incident. Une fente collectrice est placée entre M et N et a pour largeur L 0 dans le plan de la figure. Les chambres sont sous vide. On négligera le poids des ions devant les autres forces. Quel doit être le signe de la tension VG1-VG2 pour que les ions soient accélérés entre O1 et O2 ? th. de l'énergie
cinétique entre G1 et G2 :
le poids est négligeable devant la force électrique ; le travail de la force électrique est : q (VG1-VG2)
;
ce travail doit être moteur pour que les ions soient
accélérés : or q=e, charge positive des ions, donc VG1-VG2 >0.
Etablir les expressions des vitesses des ions
lorsqu'ils arrivent en O2 en fonction de m1,
m2, e et U= VG1-VG2. La vitesse initiale en G 1
est
nulle ½ m i v² i-
0 = e U d'où v²i
= 2 e U / mi ; vi
=[2 e U / mi]½
avec i =1, 2. L'énergie acquise par les ions en O 2 est 15,0 keV. En déduire U ainsi que les vitesses. m 1 = 3,90 10 -25 kg ; m2 = 3,95 10-25 kg. E c finale = e U ; U = 15,0 10 3 V = 15,0 V. v 1 =(2*1,6 10 -19 *15,0 10 3 / ( 3,90 10-25)) ½ =1,109 10 5 ~1,11 10 5 m/s. v2 =(2*1,6 10-19 *15,0 103 / (3,95 10-25))½ =1,1024 105 ~1,10 105 m/s.
Quel doit être le sens du champ magnétique,
régnant
dans la chambre de déviation,
pour que les ions puissent atteindre
le collecteur ? 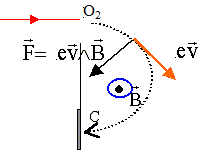
Montrer que la trajectoire de chaque type d'ion est
un cercle dont on donnera le rayon R1 (
respectivement R2) en fonction de m1
( respectivement m2), e, B et U.
Dans la chambre de déviation, la force est
perpendiculaire au vecteur vitesse et au vecteur champ magnétique : la
trajectoire des ions est plane et située dans un plan perpendiculaire au champ
et contenant le vecteur vitesse.
La force électromagnétique est à chaque instant
perpendiculaire au vecteur vitesse. Cette force ne travaille pas et ne modifie
pas l'énergie cinétique de la particule chargée. La norme du vecteur vitesse est constante : mouvement
uniforme.
Dans le repère de Frenet écrire la seconde loi de Newton
sur l'axe n.
la particule chargée n'est soumise qu'à la force de
Lorentz, centripète.
d'où eviB= mivi
2/ Ri soit Ri
= mivi /(eB)
or vi =[2
e U / mi]½ ;
Ri =[2 mi
U / (eB2)]½
avec i = 1, 2. Ri est constant : la trajectoire
est un cercle.
Quelle doit être la valeur du champ magnétique pour collecter 235U+ à D = 940 mm de O2.
R1 = ½D = 0,47 m ;
R1 =[2 m1
U / (eB2)]½ ; B = (2 m1
U / e)½/R1 =(2*3,90 10-25 *15 103 /(1,6 10-19))½/0,47 = 0,575 T.
La fente du collecteur a une largeur L0 = 4,0 mm. Peut-il y avoir séparation isotopique dans le collecteur ?
R2 =[2 m2
U / (eB2)]½ = (2*3,95 10-25 *15 103 /(1,6 10-19*0,575))½ = 0,4733 m.
Les ions 238U+ sont collectés à 473,3*2 = 946,6 ~947 mm de O2. La séparation des ions est donc possible.
L'intensité du faisceau utilisé est de 100 mA. La source est alimentée en uranium contenant 0,7 % d'23592U+.
Quelle masse m d'uranium 235 le spectrographe peut-il isoler en une année de fonctionnement continu ?
Q =I Dt = 0,100 * 365*24*3600 =3,1536 106 C.
Quantité de matière d'ion : Q / F =3,1536 106 /96500 =32,68 mol ;
soit 32,68 *0,7 / 100 = 0,2287 mol d'uranium 235 ou 0,2287*235 = 53,8 g.
|
| .
. |
|
|
Capteur de température.
On construit une chaîne
électronique avec trois amplificateurs
opérationnels. La tension v(q)
est fournie par un capteur de température qui ne peut
délivrer de courant électrique. Cette tension
est seulement fonction de la température
q
et elle est donnée avec précision par : v(q)
= v0-aq.
avec v0=0,7 V et a= 2mV
°C-1, les résistances ont pour
valeurs R1=2 kW
et R2 = 1 kW.
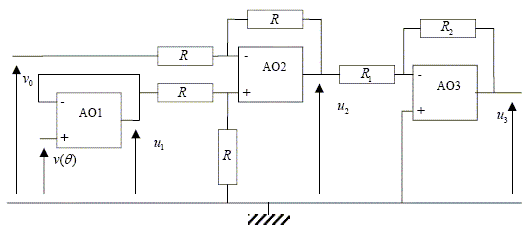
Les trois amplificateurs sont supposés parfaits et
fonctionnent en régime linéaire :
rappeler les
caractéristiques de tels
amplificateurs.
Les tensions d'entrée V+ et
V- sont égales ; les intensités des
courants d'entrée sont nulles.
Quelle relation y a-t-il entre
u1 et v(q)
? Quel est le rôle de ce premier étage
(AO1) ?
Le premier étage est un montage suiveur :
u1=v(q).
Le capteur de température ne peut pas fournir de
courant : l'étage n°1 permet de garder la
tension fournie par le capteur et délivre un courant
à la sortie.
Exprimer
u2 en fonction de v0 et
u1 , puis en déduire u2
en fonction de la température
q.
Théorème de Millman :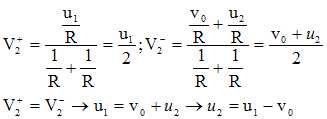 Etage soustracteur ; or
u1=v(q)
et
v(q)
= v0-aq
d'où u2 =
-aq.
Exprimer u3 en
fonction de u2. En déduire la relation
entre u3 et la température
q. 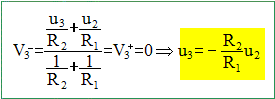
u3 =
R2/R1
aq.
Quel est
l’intérêt d’utiliser un
millivoltmètre pour mesurer la tension de
sortie du
montage.
R2/R1
= 0,5 ; a = 2 mV °C-1 ; u3 =
q.
avec u3 en mV et q
en °C.
La lecture de la tension
en mV donne la température en
°C.
|
.
|
|
Cycle de Brayton.
Un
gaz parfait, ici de l'hélium circule dans une installation. Il échange
du travail avec l'extérieur uniquement dans le compresseur et dans la
turbine. Le travail du gaz par le passage dans la turbine sert, d'une
part à faire fonctionner le compresseur ( turbine et compresseur montés
sur le même axe ) et d'autre part, à fabriquer de l'électricité. On
suppose que les transferts thermiques ont lieu exclusivement dans les
échangeurs.
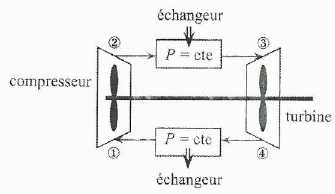
Le cycle est constitué de deux isobares et de 2 isentropes ( ou nadiabatiques réversibles ).
- compression adiabatique réversible dans le compresseur du point 1 ( T1=300K ; P1=20 bar ) vers le point 2 ( P2 = 80 bar ) ;
- détente isobare dans l'échangeur du point 2 vers le point 3 ( T3=1,30 103 K) ;
- détente adiabatique réversible dans la turbine de 3 vers 4 ( de P3=P2 à P4=P1 ) ;
- compression isobare dans l'échangeur de 4 vers 1.
On donne pour l'hélium Cvm = 1,5 R et Cpm = 2,5 R.
Pour une transformation isentropique PVg = K = constante.
Montrer que T/Pß = K' = constante ; exprimer ß en fonction de g.
PV = nRT ; V = nRT/P ; PVg =P (nRT)g/ Pg ; P(1-g) Tg = 1/(nR)g = K' ; T P(1-g)/g =K' ; T / P(g-1)/g =K' ; ß =( g-1)/g.
Déterminer les températures T2 et T4.
T1 / P1(g-1)/g =T2 / P2(g-1)/g ; T2 =T1 (P2/P1)(g-1)/g avec g = Cpm / Cvm = 1,67. T2 = 300*40,4 =522,3 ~522 K.
T3 / P3(g-1)/g =T4 / P4(g-1)/g ; T4 =T3 (P4/P3)(g-1)/g . T4 = 1,30 103*0,250,4 =746,65 ~747 K.
Tracer l'allure du cycle de Brayton du moteur sur un diagrammme (P, V).
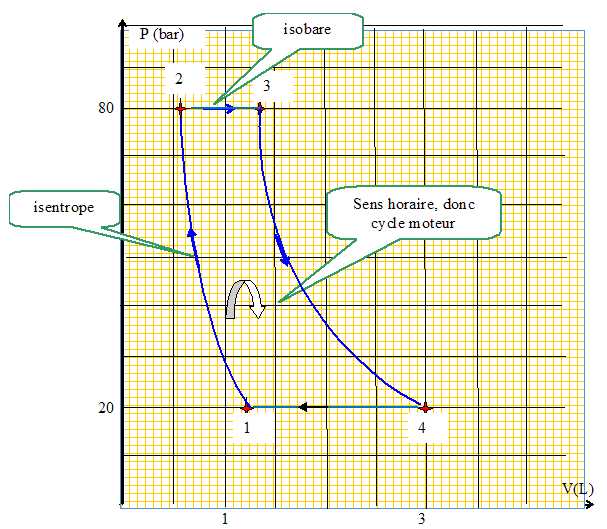
Exprimer puis calculer les transferts thermiques Q23 et Q41 pour une mole d'hélium.
Les travaux sont nulles ; " le fluide échange
du travail avec l'extérieur uniquement dans le compresseur et dans la
turbine".
Q23 = Cpm( T3-T2) =2,5R( T3-T2) =2,5*8,31(1300-522) =16162 ~16,1 kJ
Q41 = Cpm( T4-T1) =2,5R( T1-T4) =2,5*8,31(300-747) = -9286 ~ -9,29 kJ.
A partir du premier principe pour un écoulement de fluide en régime
stationnaire où le fluide circule lentement et horizontalement,
calculer les travaux W12 et W34 pour une mole d'hélium. Q12 =Q34 =0 transformations adiabatiques réversibles.
On négligera les variations d'énergie cinétique et potentielle du fluide.
On note V le volume du fluide et W le travail échangé entre le système et l'extérieur.
dU = dW+dQ = -PdV +dQ ; dH = dU + d(PV) = -PdV +dQ +VdP+PdV ; dH = VdP +dQ = -dWP+ dQ. Par suite : h2-h1 = W12+Q12 = W12.
Sur le cycle : 0 = W + Q23 +Q41 ; W = -(Q23 +Q41 ) = 9,29-16,1 = -6,81 kJ.
Montrer que le rendement du moteur peut se mettre sous la forme h = 1-(P1/P2)-ß. On pose a = P2/P1.
Rendement =|W| / Q23 = (Q23 +Q41 ) / Q23 =1- Q41 / Q23 =1-( T4-T1) /( T3-T2).
adiabatique réversible 1 --> 2 : T1 P1(1-g)/g = T2 P2(1-g)/g ; adiabatique réversible 3 --> 4 : T3 P3(1-g)/g = T4 P4(1-g)/g ;
Or P2 = P3 et P4 = P1 : T3 P2(1-g)/g = T4 P1(1-g)/g ;
T1 = T2 a(1-g)/g ; T4 = T3 a(1-g)/g ; T4-T1 = (T3 -T2 )a(1-g)/g ; rendement = 1-a(1-g)/g .
Calculer ce rendement et le comparer au rendement de Carnot obtenu en utilisant les deux températures extrèmes du système.
hCarnot = 1-Tf/Tc = 1-300/1300 ~ 0,77.
h = 1-(P1/P2)ß=1-(20/80)0,4 =0,43, inférieur au rendement de Carnot.
|
|
|